题目内容
（1）化简求值：（a+b）（a-b）+b（a+2b）-b2，其中a=1，b=-2
（2）实数范围内分解因式：x4-4．
（2）实数范围内分解因式：x4-4．
考点：整式的混合运算—化简求值,实数范围内分解因式
专题：计算题
分析：（1）原式第一项利用平方差公式计算，第二项利用单项式乘以多项式法则计算，去括号合并得到最简结果，把a与b的值代入计算即可得到结果；
（2）原式利用平方差公式分解即可．
（2）原式利用平方差公式分解即可．
解答：解：（1）原式=a2-b2+ab+2b2-b2=a2+ab，
当a=1，b=-2时，原式=1-2=-1；
（2）原式=（x2+2）（x+
）（x-
）．
当a=1，b=-2时，原式=1-2=-1；
（2）原式=（x2+2）（x+
| 2 |
| 2 |
点评：此题考查了整式的混合运算-化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
已知关于x的一次函数y=（m-2）x+n+3的图象不经过第二象限，则代数式m+2|n-m|-
可化简为（ ）
| n2 |
| A、n-m | B、3n |
| C、3m-n | D、3m |
下列合并同类项正确的是（ ）
| A、3a2-2a2=1 | ||||||
B、
| ||||||
| C、a2b-2ab2=-a2b2 | ||||||
D、-0.75m2n+
|
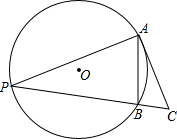如图，⊙O的半径为1，弦AB=1，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|