题目内容
 如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为
如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造关系式求解.
解答: 解:过点C作CE⊥AB于E.
解:过点C作CE⊥AB于E.
∵∠ADC=90°-60°=30°,∠ACD=90°-30°=60°,
∴∠CAD=90°.
∵CD=9.6,
∴AC=
CD=4.8.
在Rt△ACE中,∵∠AEC=90°,∠ACE=30°,
∴AE=
AC=2.4,
CE=AC•cos∠ACE=4.8•cos30°=
.
在Rt△BCE中,∵∠BCE=45°,
∴BE=CE=
,
∴AB=AE+BE=2.4+
≈6.6(米).
即雕塑AB的高度约为6.6米.
故答案为6.6.
 解:过点C作CE⊥AB于E.
解:过点C作CE⊥AB于E.∵∠ADC=90°-60°=30°,∠ACD=90°-30°=60°,
∴∠CAD=90°.
∵CD=9.6,
∴AC=
| 1 |
| 2 |
在Rt△ACE中,∵∠AEC=90°,∠ACE=30°,
∴AE=
| 1 |
| 2 |
CE=AC•cos∠ACE=4.8•cos30°=
12
| ||
| 5 |
在Rt△BCE中,∵∠BCE=45°,
∴BE=CE=
12
| ||
| 5 |
∴AB=AE+BE=2.4+
12
| ||
| 5 |
即雕塑AB的高度约为6.6米.
故答案为6.6.
点评:本题考查了解直角三角形的应用-仰角俯角问题,要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
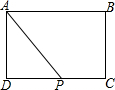 如图,在长方形ABCD中,AB=6,AD=4,P是CD上的动点,且不与点C,D重合,设DP=x,梯形ABCP的面积为y,则y与x之间的函数关系式和自变量的取值范围分别是( )
如图,在长方形ABCD中,AB=6,AD=4,P是CD上的动点,且不与点C,D重合,设DP=x,梯形ABCP的面积为y,则y与x之间的函数关系式和自变量的取值范围分别是( )| A、y=24-2x;0<x<6 |
| B、y=24-2x;0<x<4 |
| C、y=24-3x;0<x<6 |
| D、y=24-3x;0<x<4 |
 如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0)、(0,2),以点A为圆心,以AB为长为半径画弧,交x正半轴于点C,则点C的坐标为
如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0)、(0,2),以点A为圆心,以AB为长为半径画弧,交x正半轴于点C,则点C的坐标为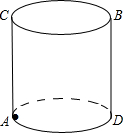 如图,圆柱的高为10cm,底面半径为4cm,在圆柱下底面的A点处有一只蚂蚁,它想吃到上底面B处的食物,已知四边形ADBC的边AD、BC恰好是上、下底面的直径.为:蚂蚁至少要爬行多少路程才能食到食物?
如图,圆柱的高为10cm,底面半径为4cm,在圆柱下底面的A点处有一只蚂蚁,它想吃到上底面B处的食物,已知四边形ADBC的边AD、BC恰好是上、下底面的直径.为:蚂蚁至少要爬行多少路程才能食到食物? 如图,正方形ABCD的对角线BD是菱形BEFD的一边,菱形BEFD的对角线BF交于P,则∠BPD的度数为
如图,正方形ABCD的对角线BD是菱形BEFD的一边,菱形BEFD的对角线BF交于P,则∠BPD的度数为 如图,P是正方形ABCD内一点,如果△ABP为等边三角形,DP的延长线交BC于G,那么∠PCD=
如图,P是正方形ABCD内一点,如果△ABP为等边三角形,DP的延长线交BC于G,那么∠PCD=