题目内容
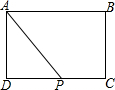 如图,在长方形ABCD中,AB=6,AD=4,P是CD上的动点,且不与点C,D重合,设DP=x,梯形ABCP的面积为y,则y与x之间的函数关系式和自变量的取值范围分别是( )
如图,在长方形ABCD中,AB=6,AD=4,P是CD上的动点,且不与点C,D重合,设DP=x,梯形ABCP的面积为y,则y与x之间的函数关系式和自变量的取值范围分别是( )| A、y=24-2x;0<x<6 |
| B、y=24-2x;0<x<4 |
| C、y=24-3x;0<x<6 |
| D、y=24-3x;0<x<4 |
考点:函数关系式,函数自变量的取值范围
专题:
分析:根据DP=x可得CP=6-x,再根据梯形的面积公式代入相应数值进行计算即可.
解答:解:∵DP=x,
∴CP=6-x,
∴y=
(AB+CP)•BC=
(6+6-x)•4=2(12-x)=24-2x,
∵P是CD上的动点,且不与点C,D重合,
∴0<x<6,
故选:A.
∴CP=6-x,
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
∵P是CD上的动点,且不与点C,D重合,
∴0<x<6,
故选:A.
点评:此题主要考查了根据实际问题列函数关系式,关键是掌握梯形的面积公式.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
在?ABCD中,∠A:∠B:∠C:∠D的值可能是( )
| A、1:2:1:2 |
| B、1:3:3:1 |
| C、2:3:1:4 |
| D、1:2:3:4 |
下列运算中与a4•a4结果相同的是( )
| A、a2•a8 |
| B、(a2)4 |
| C、(a4)4 |
| D、(a2)4•(a2)4 |
已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠C等于( )
| A、120° | B、80° |
| C、60° | D、40° |
若|m+3|+(n-5)2=0,则关于x,y的二元一次方程组
的解为( )
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为
如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为