题目内容
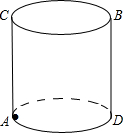 如图,圆柱的高为10cm,底面半径为4cm,在圆柱下底面的A点处有一只蚂蚁,它想吃到上底面B处的食物,已知四边形ADBC的边AD、BC恰好是上、下底面的直径.为:蚂蚁至少要爬行多少路程才能食到食物?
如图,圆柱的高为10cm,底面半径为4cm,在圆柱下底面的A点处有一只蚂蚁,它想吃到上底面B处的食物,已知四边形ADBC的边AD、BC恰好是上、下底面的直径.为:蚂蚁至少要爬行多少路程才能食到食物?考点:平面展开-最短路径问题
专题:
分析:求至少要爬多少路程,根据两点之间直线最短,把圆柱体展开,在得到的矩形上连接两点,求出距离即可.
解答: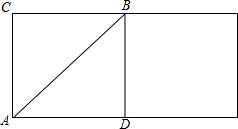 解:把圆柱体沿着AC直线剪开,得到矩形如下:
解:把圆柱体沿着AC直线剪开,得到矩形如下:
则AB的长度为所求的最短距离,
根据题意圆柱的高为10cm,底面半径为4cm,
则可以知道AC=10cm,BC=
底面周长,
∵底面周长为2πr=2×π×4=8πcm,
∴BC=4πcm,
根据勾股定理得AB2=AC2+BC2,
即AB2=102+(4π)2,
∴AB=
=2
cm.
答:蚂蚁至少要爬行2
cm路程才能食到食物.
 解:把圆柱体沿着AC直线剪开,得到矩形如下:
解:把圆柱体沿着AC直线剪开,得到矩形如下:则AB的长度为所求的最短距离,
根据题意圆柱的高为10cm,底面半径为4cm,
则可以知道AC=10cm,BC=
| 1 |
| 2 |
∵底面周长为2πr=2×π×4=8πcm,
∴BC=4πcm,
根据勾股定理得AB2=AC2+BC2,
即AB2=102+(4π)2,
∴AB=
| 100+16π2 |
| 25+4π2 |
答:蚂蚁至少要爬行2
| 25+4π2 |
点评:本题考查平面展开最短路径问题,关键知道圆柱展开图是长方形,根据两点之间线段最短可求出解.

练习册系列答案
相关题目
 河南商报报道,2013年夏季,河南省境内大面积干旱,水库的蓄水量普遍下降,如图表示的是某水库的蓄水量V(立方万米)与干旱持续时间t(天)之间的函数关系的图象,请根据此图象,回答下列问题:
河南商报报道,2013年夏季,河南省境内大面积干旱,水库的蓄水量普遍下降,如图表示的是某水库的蓄水量V(立方万米)与干旱持续时间t(天)之间的函数关系的图象,请根据此图象,回答下列问题: 如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=126°,则∠DBC的度数为
如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=126°,则∠DBC的度数为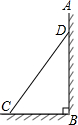 如图,铁管CD固定在墙角,BC=5米,∠BCD=55°,则顶端D的高度为
如图,铁管CD固定在墙角,BC=5米,∠BCD=55°,则顶端D的高度为 如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为
如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为