题目内容
13. 如图,已知在平面直角坐标系中,点B在x轴上,半径为3的⊙B与y轴相切,直线l过点A(-2,0),且和⊙B相切,与y轴相交于点C.若点E在直线l上,且以A为圆心,AE为半径的圆与⊙B相切,求点E的坐标.
如图,已知在平面直角坐标系中,点B在x轴上,半径为3的⊙B与y轴相切,直线l过点A(-2,0),且和⊙B相切,与y轴相交于点C.若点E在直线l上,且以A为圆心,AE为半径的圆与⊙B相切,求点E的坐标.
分析 分两种情形讨论即可①当⊙A与⊙B内切时,直线l与⊙A交于点E1、E2,作E1M⊥x轴于M.设⊙B与直线l相切于点D,连接BD,则BD⊥直线l,则AE1=8.
②当⊙A与⊙B外切时,⊙A与直线l交于点E2、E3,作E2N⊥x轴于N.则AE2=2,利用相似三角形的性质分别求解即可.
解答 解:如图,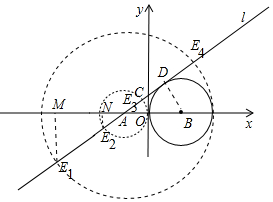
①当⊙A与⊙B内切时,直线l与⊙A交于点E1、E2,作E1M⊥x轴于M.设⊙B与直线l相切于点D,连接BD,则BD⊥直线l,
在RtADB中,AB=5,BD=3,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵⊙A与⊙B内切,
∵AE1=8,
∵∠MAE1=∠DAB,∠E1MA=∠BDA,
∴△AME1∽△ADB,
∴$\frac{AM}{AD}$=$\frac{{E}_{1}M}{BD}$=$\frac{A{E}_{1}}{AB}$,
∴$\frac{AM}{4}$=$\frac{{E}_{1}M}{3}$=$\frac{8}{5}$,
∴AM=$\frac{32}{5}$,E1M=$\frac{24}{5}$,
∴OM=$\frac{42}{5}$,点E1(-$\frac{42}{5}$,-$\frac{24}{5}$),
∵E4与E1关于点A对称,
∴E4($\frac{22}{5}$,-$\frac{24}{5}$).
②当⊙A与⊙B外切时,⊙A与直线l交于点E2、E3,作E2N⊥x轴于N.则AE2=2,
由△ANE2∽△ADB,可得$\frac{AN}{AD}$=$\frac{N{E}_{2}}{BD}$=$\frac{A{E}_{2}}{AB}$,
∴$\frac{AN}{4}$=$\frac{N{E}_{2}}{3}$=$\frac{2}{5}$,
∴AN=$\frac{8}{5}$,NE2=$\frac{6}{5}$,ON=$\frac{18}{5}$,
∴E2(-$\frac{18}{5}$,-$\frac{6}{5}$).
∵E2与E3关于点A对称,
∴E3(-$\frac{2}{5}$,$\frac{6}{5}$).
综上所述,点E的坐标为(-$\frac{42}{5}$,-$\frac{24}{5}$)或($\frac{22}{5}$,$\frac{24}{5}$)或(-$\frac{18}{5}$,-$\frac{6}{5}$)或(-$\frac{2}{5}$,$\frac{6}{5}$).
点评 本题考查切线的性质、两圆的位置关系、相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.

| A. | 抽到方块8 | B. | 抽到K牌 | C. | 抽到梅花 | D. | 抽到大王 |
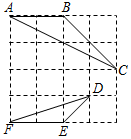 如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB的值为( )
如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 3 |
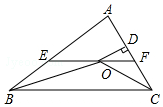 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论: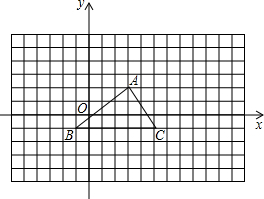 如图所示的网格中,每个小方格都是边长为1的正方形,B点的坐标为(-1,-1).
如图所示的网格中,每个小方格都是边长为1的正方形,B点的坐标为(-1,-1).