题目内容
16.在一个不透明的盒子中装有涂颜色不同的8个小球,其中红球3个,黑球5个.(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
| 事件A | 必然事件 | 随机事件 |
| m的值 | 3 | 2 |
分析 (1)根据必然事件、不可能事件、随机事件的概念解答;
(2)利用概率公式计算即可.
解答 解:(1)从袋中取出3个红球,再从袋中随机摸出1个球,“摸出黑球”是必然事件,
从袋中取出2个红球,再从袋中随机摸出1个球,“摸出黑球”是随机事件,
故答案为:3;2;
(2)由题意得,$\frac{m+5}{8}$=$\frac{3}{4}$,
解得,m=1.
点评 本题考查的是随机事件的定义、概率的求法,必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.

练习册系列答案
相关题目
7.下列结论中,错误的是( )
| A. | 经过直线外一点,有且只有一条直线与这条直线平行 | |
| B. | 如果直线a,b,c满足:a∥b,c∥b,那么a∥c | |
| C. | 如果一个角的两边与另一个角的两边分别平行,那么这两个角相等 | |
| D. | 从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离 |
11. 如图,G是正方形形ABCD的边BC上一点,DE、BF分别垂直AG于点E、F,则图中与△ABF相似的三角形有( )
如图,G是正方形形ABCD的边BC上一点,DE、BF分别垂直AG于点E、F,则图中与△ABF相似的三角形有( )
 如图,G是正方形形ABCD的边BC上一点,DE、BF分别垂直AG于点E、F,则图中与△ABF相似的三角形有( )
如图,G是正方形形ABCD的边BC上一点,DE、BF分别垂直AG于点E、F,则图中与△ABF相似的三角形有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.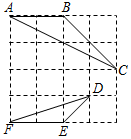 如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB的值为( )
如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB的值为( )
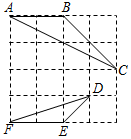 如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB的值为( )
如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 3 |
6.从2开始,连续的偶数相加,它们的和的情况如下表:
(1)如果n=8时,那么S的值为72;
(2)根据表中的规律猜想:用n的代数式表示S的公式为S=2+4+6+8+…+2n=n(n+1);
(3)由上题的规律计算100+102+104+…+2014+2016的值(要有计算过程)
| 加数的个数n | 连续偶数的和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
(2)根据表中的规律猜想:用n的代数式表示S的公式为S=2+4+6+8+…+2n=n(n+1);
(3)由上题的规律计算100+102+104+…+2014+2016的值(要有计算过程)
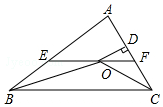 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论: