题目内容
14.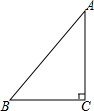 在Rt△ABC中,AB=10cm,BC=6cm,AC=8cm,问以点C为圆心,r为半径的⊙C与直线AB有怎样的位置关系:
在Rt△ABC中,AB=10cm,BC=6cm,AC=8cm,问以点C为圆心,r为半径的⊙C与直线AB有怎样的位置关系:(1)r=4cm;
(2)r=4.8cm;
(3)r=6cm.
分析 过点C作CD⊥AB于点D,根据三角形的面积公式求出CD的长,再由直线与圆的位置关系即可得出结论.
解答  解:过点C作CD⊥AB于点D.
解:过点C作CD⊥AB于点D.
则CD=$\frac{AC•BC}{AB}$=4.8(cm).
(1)∵当r=4cm时,CD>r,∴⊙C与直线AB相离.
(2)∵当r=4.8cm时,CD=r,∴⊙C与直线AB相切.
(3)∵当r=6cm时,CD<r,∴⊙C与直线AB相交.
点评 本题考查的是直线与圆的位置关系,熟知直线和圆的三种位置关系是解答此题的关键.

练习册系列答案
相关题目
4.地球绕着太阳公转的速度约为110000千米/时,这个数用科学记数法表示为( )
| A. | 11×104千米/时 | B. | 1.1×104千米/时 | C. | 1.1×105千米/时 | D. | 1.1×106千米/时 |
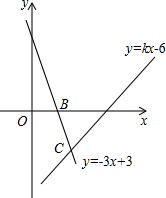 如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.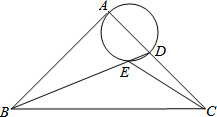 如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=$4\sqrt{2}$,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为2$\sqrt{5}$-2.
如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=$4\sqrt{2}$,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为2$\sqrt{5}$-2.




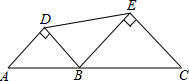 如图,A、B、C三点在同一直线上,以AB、BC为斜边分别作等腰直角三角形ABD和BCE,连接DE.若AC=4,则DE的取值范围是2≤DE$<2\sqrt{2}$.
如图,A、B、C三点在同一直线上,以AB、BC为斜边分别作等腰直角三角形ABD和BCE,连接DE.若AC=4,则DE的取值范围是2≤DE$<2\sqrt{2}$. 已知某企业2014年用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某企业2014年用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.