题目内容
6.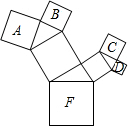 若图中正方形F以上的正方形均是以直角三角形向外作的正方形:
若图中正方形F以上的正方形均是以直角三角形向外作的正方形:(1)若正方形A,B,C,D的边长分别是a,b,c,d,则正方形F的面积如何用a,b,c,d的式子表示出来为F的面积=a2+b2+c2+d2;
(2)如果正方形F的边长16cm,那么正方形A,B,C,D的面积之和是256cm2.
分析 (1)如图所示;由勾股定理可知:SA+SB=SG,SC+SD=SE,SG+SE=SF,从而可求得正方形F的面积;
(2)由(1)可知SF=SA+SB+SC+SD,从而可求得答案.
解答 解:如图所示:
(1)由勾股定理得:SA+SB=SG,SC+SD=SE,SG+SE=SF,
∴SF=SA+SB+SC+SD=a2+b2+c2+d2.
(2)正方形A,B,C,D的面积之和=SF=16×16=256cm2.
点评 本题主要考查的是勾股定理的应用,掌握勾股定理是解题的关键.

练习册系列答案
相关题目
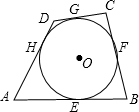 如图,四边形ABCD外切于⊙O,切点分别是E、F、G、H.
如图,四边形ABCD外切于⊙O,切点分别是E、F、G、H. 如图,已知AB∥ED,∠B=50°,CN是∠BCE的平分线,CM⊥CN,求∠MCD的度数.
如图,已知AB∥ED,∠B=50°,CN是∠BCE的平分线,CM⊥CN,求∠MCD的度数.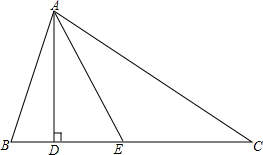 如图,△ABC中,∠B>∠C,AD是高,AE平分∠BAC,求证:∠DAE=$\frac{1}{2}$(∠B-∠C).
如图,△ABC中,∠B>∠C,AD是高,AE平分∠BAC,求证:∠DAE=$\frac{1}{2}$(∠B-∠C).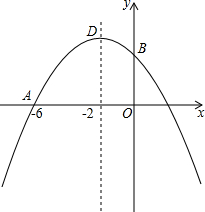 已知抛物线y=ax2-x+c过点A(-6,0),对称轴是直线x=-2,与y轴交于点B,顶点为D.
已知抛物线y=ax2-x+c过点A(-6,0),对称轴是直线x=-2,与y轴交于点B,顶点为D.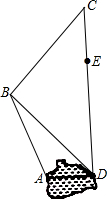 如图是某个园区部分景点(景点A,B,C,D,E)示意图,景点A,D之间是一个荷花池,景点E,D和景点B,D之间正在维修,不能通行.已知AB=400$\sqrt{3}$米,BC=l000米,CE=600米,CD⊥AD,∠BDC=45°,∠ABD=15°.请根据以上条件求出荷花池AD的宽度和景点E,D之间的距离.
如图是某个园区部分景点(景点A,B,C,D,E)示意图,景点A,D之间是一个荷花池,景点E,D和景点B,D之间正在维修,不能通行.已知AB=400$\sqrt{3}$米,BC=l000米,CE=600米,CD⊥AD,∠BDC=45°,∠ABD=15°.请根据以上条件求出荷花池AD的宽度和景点E,D之间的距离.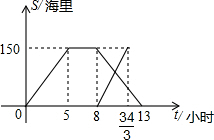 黄岩岛是我国南沙群岛的一个小岛,一天某渔船在该海域捕鱼,突然发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告并立即返航,渔政船接到报告后,立即出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t的函数图象.(假设渔船和渔政船沿同一航线航行)则在渔政船驶往黄岩岛的过程中,渔船从港口出发经过9.6或10.4小时与渔政船相距30海里.
黄岩岛是我国南沙群岛的一个小岛,一天某渔船在该海域捕鱼,突然发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告并立即返航,渔政船接到报告后,立即出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t的函数图象.(假设渔船和渔政船沿同一航线航行)则在渔政船驶往黄岩岛的过程中,渔船从港口出发经过9.6或10.4小时与渔政船相距30海里.