题目内容
17.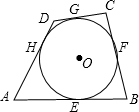 如图,四边形ABCD外切于⊙O,切点分别是E、F、G、H.
如图,四边形ABCD外切于⊙O,切点分别是E、F、G、H.(1)请探索四边形ABCD四边AB、BC、CD、AD之间的关系;
(2)圆的外切平行四边形是菱形;
(3)圆的外切矩形是正方形;
(4)若AB:BC:CD:DA=1:3:4:x,且四边形ABCD的周长为20cm,则x=2,AD=4cm.
分析 (1)利用切线长定理进而得出AH=AE,BE=BF,CF=CG,DG=DH,即可得出AB、BC、CD、AD之间的关系;
(2)利用(1)中所求,结合平行四边形和菱形的性质得出答案;
(3)利用(1)中所求,结合矩形和正方形的性质得出答案;
(4)利用(1)中所求,首先求出x的值,进而得出AD的长.
解答 解:(1)∵四边形ABCD外切于⊙O,切点分别是E、F、G、H,
∴AH=AE,BE=BF,CF=CG,DG=DH,
∴AH+DH+CF+BF=DG+CG+AE+BE,
即AD+BC=AB+DC;
(2)由(1)得,圆的外切四边形对边和相等,
则圆的外切平行四边形是:菱形;
故答案为:菱;
(3)由(1)得,圆的外切四边形对边和相等,
则圆的外切矩形是正方形;
故答案为:正方;
(4)∵AB:BC:CD:DA=1:3:4:x,AD+BC=AB+DC,
∴1+4=3+x,
则x=2,
∵四边形ABCD的周长为20cm,
∴20÷(1+3+4+2)=2,
∴AD=2×2=4(cm).
故答案为:2,4cm.
点评 此题主要考查了切线长定理以及矩形、菱形、平行四边形的性质等知识,熟练应用切线长定理是解题关键.

练习册系列答案
相关题目
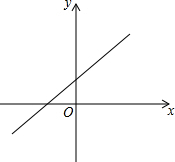 已知二次函数y1=x2-2x-3及一次函数y2=x+m,将该二次函数图象在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象,求新图象与直线y2=x+m有三个不同公共点时m的值1或$\frac{13}{4}$.
已知二次函数y1=x2-2x-3及一次函数y2=x+m,将该二次函数图象在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象,求新图象与直线y2=x+m有三个不同公共点时m的值1或$\frac{13}{4}$.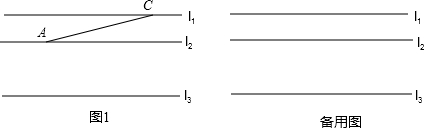
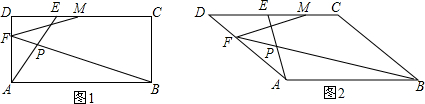
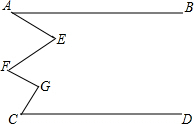 如图,已知直线AB∥CD,试确定∠A,∠F,∠C与∠E,∠G之间的数量关系并说明理由.
如图,已知直线AB∥CD,试确定∠A,∠F,∠C与∠E,∠G之间的数量关系并说明理由. 如图,B坐标为(2,0),AB⊥x轴于B,△ABO的面积为3.
如图,B坐标为(2,0),AB⊥x轴于B,△ABO的面积为3.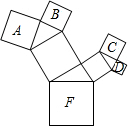 若图中正方形F以上的正方形均是以直角三角形向外作的正方形:
若图中正方形F以上的正方形均是以直角三角形向外作的正方形: