题目内容
8. 已知实数a、b、c在数轴上位置如图所示.试化简:$\sqrt{(a-c)^{2}}$-($\sqrt{c-b}$)2-|b-a|.
已知实数a、b、c在数轴上位置如图所示.试化简:$\sqrt{(a-c)^{2}}$-($\sqrt{c-b}$)2-|b-a|.
分析 利用$\sqrt{{a}^{2}}$=|a|,再利用绝对值的性质可得答案.
解答 解:原式=|a-c|-|c-b|-|b-a|,
=c-a-(c-b)-(b-a),
=c-a-c+b-b+a,
=2c.
点评 此题主要考查了绝对值和二次根式的性质,关键是掌握$\sqrt{{a}^{2}}$=|a|,掌握非负数的绝对值等于它本身.

练习册系列答案
相关题目
18.3的相反数是( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | -3 | D. | -1 |
 如图,已知∠E=∠F,∠B=∠D,试说明∠D=∠1的理由.
如图,已知∠E=∠F,∠B=∠D,试说明∠D=∠1的理由. 如图,在4×4的方格图中,每个小正方形的边长都为1.图中阴影是个正方形,顶点均在格点上,则这个正方形的边长是$\sqrt{10}$.
如图,在4×4的方格图中,每个小正方形的边长都为1.图中阴影是个正方形,顶点均在格点上,则这个正方形的边长是$\sqrt{10}$.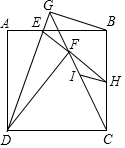 如图,E为正方形ABCD边AB上的一点,且AD=3,AE=1,将△ADE沿DE翻折得到△FDE,连接并延长CF与DE延长线相交于点G,连接BG,延长EF交BC于H,过点H作HI∥BG,则HI的长为$\frac{3}{10}$$\sqrt{10}$.
如图,E为正方形ABCD边AB上的一点,且AD=3,AE=1,将△ADE沿DE翻折得到△FDE,连接并延长CF与DE延长线相交于点G,连接BG,延长EF交BC于H,过点H作HI∥BG,则HI的长为$\frac{3}{10}$$\sqrt{10}$.