题目内容
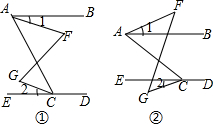
3. 如图,已知∠E=∠F,∠B=∠D,试说明∠D=∠1的理由.
如图,已知∠E=∠F,∠B=∠D,试说明∠D=∠1的理由.
分析 连接AC,由∠E=∠F可得出AB∥CD、∠BAC=∠DCA,结合∠B=∠D利用三角形内角和定理可得出∠BCA=∠DAC,利用“内错角相等,两直线平行”可得出BC∥AD,再根据平行线的性质即可得出∠D=∠1.
解答 解:连接AC,如图所示.
∵∠E=∠F,
∴AB∥CD,
∴∠BAC=∠DCA.
∵∠B=∠D,∠BAC+∠BCA+∠B=180°,∠DCA+∠DAC+∠D=180°,
∴∠BCA=∠DAC,
∴BC∥AD,
∴∠D=∠1.
点评 本题考查了平行线的判定与性质以及三角形内角和定义,根据平行线的性质结合三角形内角和定理找出∠BCA=∠DAC是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
18.从一个袋中摸出一个球(袋中每一个球被摸到的可能性相等),恰为红球的概率为$\frac{1}{4}$,若袋中原有红球4个,则袋中球的总数大约是( )
| A. | 32个 | B. | 24个 | C. | 16个 | D. | 12个 |
19.南京江北新区包括南京市浦口区、六合区和栖霞区部分街道,规划面积788 000 000平方米.用科学记数法表示788 000 000是( )
| A. | 0.788×108 | B. | 7.88×108 | C. | 7.88×109 | D. | 788×106 |
12. 下表1为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,如图是按照某公司购买的100张门票的种类、数量绘制的扇形图:
下表1为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,如图是按照某公司购买的100张门票的种类、数量绘制的扇形图:
依据上列图表,回答下列问题:
(1)其中观看乒乓球比赛的门票占全部门票的20%;观看足球比赛的门票有50张;
(2)购买乒乓球门票的总款数占全部门票总款数的$\frac{5}{42}$(填几分之几);
(3)奥运会期间,某售票点第二周的门票销售额为200万元,比第一周销售额增长了6%,该售票点第三周的门票销售额的增长率在第二周的基础上提高了四个百分点,
①这个售票点第三周的门票销售额为多少万元?
②这个售票点第一周的门票销售额为多少万元?(结果保留整数)
 下表1为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,如图是按照某公司购买的100张门票的种类、数量绘制的扇形图:
下表1为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,如图是按照某公司购买的100张门票的种类、数量绘制的扇形图:| 比赛项目 | 票价(元/张) |
| 足球 | 1000 |
| 男篮 | 800 |
| 乒乓球 | 500 |
(1)其中观看乒乓球比赛的门票占全部门票的20%;观看足球比赛的门票有50张;
(2)购买乒乓球门票的总款数占全部门票总款数的$\frac{5}{42}$(填几分之几);
(3)奥运会期间,某售票点第二周的门票销售额为200万元,比第一周销售额增长了6%,该售票点第三周的门票销售额的增长率在第二周的基础上提高了四个百分点,
①这个售票点第三周的门票销售额为多少万元?
②这个售票点第一周的门票销售额为多少万元?(结果保留整数)
13.已知a+b=2,则a2+4b-b2的值是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
 已知实数a、b、c在数轴上位置如图所示.试化简:$\sqrt{(a-c)^{2}}$-($\sqrt{c-b}$)2-|b-a|.
已知实数a、b、c在数轴上位置如图所示.试化简:$\sqrt{(a-c)^{2}}$-($\sqrt{c-b}$)2-|b-a|.