题目内容
10.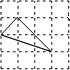 如图,每个小正方形边长均为1,则下列图中的三角形与图中△ABC相似的是( )
如图,每个小正方形边长均为1,则下列图中的三角形与图中△ABC相似的是( )| A. | 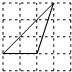 | B. | 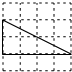 | C. | 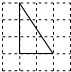 | D. | 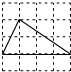 |
分析 利用网格特点和勾股定理得到AC=$\sqrt{2}$,BC2$\sqrt{2}$,AB=$\sqrt{10}$,由于($\sqrt{2}$)2+(2$\sqrt{2}$)2=($\sqrt{10}$)2,则图中△ABC为直角三角形,由于A、D选项中的三角形不是直角三角形,于是可对A、D进行判断;计算出B、C选项的直角三角形的直角边,然后根据两组对应边的比相等且夹角对应相等的两个三角形相似可对B、C进行判断.
解答 解:图中三角形三边的长分别为AC=$\sqrt{2}$,BC=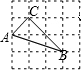 2$\sqrt{2}$,AB=$\sqrt{10}$,由于($\sqrt{2}$)2+(2$\sqrt{2}$)2=($\sqrt{10}$)2,则图中△ABC为直角三角形,
2$\sqrt{2}$,AB=$\sqrt{10}$,由于($\sqrt{2}$)2+(2$\sqrt{2}$)2=($\sqrt{10}$)2,则图中△ABC为直角三角形,
A、A选项中的三角形不是直角三角形,所以A选项错误;
B、B选项的直角三角形的直角边分别为2,4,则$\frac{2}{\sqrt{2}}$=$\frac{4}{2\sqrt{2}}$,所以B选项中的图形与△ABC相似,所以B选项正确;
C、C选项的直角三角形的直角边分别为2,3,则$\frac{2}{\sqrt{2}}$≠$\frac{3}{2\sqrt{2}}$,所以C选项中的图形与△ABC不相似,所以C选项错误;
D、D选项中的三角形不是直角三角形,所以D选项错误.
故选B.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
18.已知:a+b=m,计算a2+2ab+b2+1的结果是( )
| A. | (m+1)2 | B. | m2+1 | C. | m2 | D. | m2-1 |
 晚上,小明有路灯A走向路灯B,当他走到点P时,发现身后身后他的影子的顶部刚好接触路灯A的底部,当他向前再走12米到达Q时,发现身前他的影子的顶部刚好接触到路灯B的底部.已知,小明身高1.6米,两路灯的高AC=BD=9.6米,
晚上,小明有路灯A走向路灯B,当他走到点P时,发现身后身后他的影子的顶部刚好接触路灯A的底部,当他向前再走12米到达Q时,发现身前他的影子的顶部刚好接触到路灯B的底部.已知,小明身高1.6米,两路灯的高AC=BD=9.6米, 如图梯形ABCD中,AD∥BC,O为对角线的交点,F为OB上一点,E为CF上一点,S△AOB=10,S△BFE=3,S△BEC=9,S△OEC=6,试求梯形ABCD的面积.
如图梯形ABCD中,AD∥BC,O为对角线的交点,F为OB上一点,E为CF上一点,S△AOB=10,S△BFE=3,S△BEC=9,S△OEC=6,试求梯形ABCD的面积. 如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C.点P是x轴正半轴上的一动点,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设OP的长度为m.
如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C.点P是x轴正半轴上的一动点,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设OP的长度为m.