题目内容
18.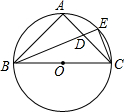 如图,⊙O是△ABC的外接圆,BC是⊙O的直径,AB=AC,∠ABC的平分线交AC于点D,交⊙O于点E,连结CE.若CE=$\sqrt{2}$,则BD的值为2$\sqrt{2}$.
如图,⊙O是△ABC的外接圆,BC是⊙O的直径,AB=AC,∠ABC的平分线交AC于点D,交⊙O于点E,连结CE.若CE=$\sqrt{2}$,则BD的值为2$\sqrt{2}$.
分析 如图,延长BA、CE交于点M,只要证明△ABD≌△ACM,△BEC≌△BEM,即可推出BD=2CE由此即可解决问题.
解答 解:如图,延长BA、CE交于点M.
∵BC是直径,∠ABD=∠ACM,
∴∠BAD=∠CAM=90°,
在△ABD和△ACM中,
$\left\{\begin{array}{l}{∠BAD=∠CAM}\\{AB=AC}\\{∠ABD=∠ACM}\end{array}\right.$,
∴△ABD≌△ACM,
∴BD=CM,
在△BEC和△BEM中,
$\left\{\begin{array}{l}{∠EBM=∠EBC}\\{BE=BE}\\{∠BEM=∠BEC}\end{array}\right.$,
∴△BEC≌△BEM.
∴EC=EM,
∴BD=CM=2CE=2$\sqrt{2}$.
故答案为2$\sqrt{2}$.
点评 本题考查三角形外接圆以及外心,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
8.B题:图①~④分别表示甲、乙两辆汽车在同一条路上匀速行驶中速度与时间的关系,小明对4个图中汽车运动的情况进行了描述,其中正确的是( )


| A. | 图①:乙的速度是甲的2倍,甲乙的路程相等 | |
| B. | 图②:乙的速度是甲的2倍,甲的路程是乙的一半 | |
| C. | 图③:乙的速度是甲的2倍,乙的路程是甲的一半 | |
| D. | 图④:甲的速度是乙的2倍,甲乙的路程相等 |
9. 如图,直线c与直线a、b相交,且a∥b,则结论:
如图,直线c与直线a、b相交,且a∥b,则结论:
①∠1=∠2;②∠3+∠4=180°;③∠3=∠2;④∠1=∠4;⑤∠4+∠2=180°;⑥∠1=∠3;
其中正确的个数为( )
 如图,直线c与直线a、b相交,且a∥b,则结论:
如图,直线c与直线a、b相交,且a∥b,则结论:①∠1=∠2;②∠3+∠4=180°;③∠3=∠2;④∠1=∠4;⑤∠4+∠2=180°;⑥∠1=∠3;
其中正确的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
13. 如图,∠1,∠2,…∠8是两条直线a,b被直线c所截后形成的八个角,则能够判定直线a∥b的是( )
如图,∠1,∠2,…∠8是两条直线a,b被直线c所截后形成的八个角,则能够判定直线a∥b的是( )
 如图,∠1,∠2,…∠8是两条直线a,b被直线c所截后形成的八个角,则能够判定直线a∥b的是( )
如图,∠1,∠2,…∠8是两条直线a,b被直线c所截后形成的八个角,则能够判定直线a∥b的是( )| A. | ∠3+∠4=180° | B. | ∠1+∠8=180° | C. | ∠5+∠7=180° | D. | ∠2+∠6=180° |
 如图,现有线段AB=2,MN=3,若在线段MN上随机取一点P,恰能使线段AB、MP、NP组成一个三角形三边的概率是$\frac{2}{3}$.
如图,现有线段AB=2,MN=3,若在线段MN上随机取一点P,恰能使线段AB、MP、NP组成一个三角形三边的概率是$\frac{2}{3}$. 按照事件发生概率的大小,将表示该事件的序号标在数轴适当位置:
按照事件发生概率的大小,将表示该事件的序号标在数轴适当位置: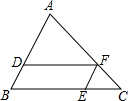 如图,在△ABC中,点D,F,E分别在边AB,AC,BC上,且DF∥BC,EF∥AB,若AD=2BD,则$\frac{CE}{BE}$的值为$\frac{1}{2}$.
如图,在△ABC中,点D,F,E分别在边AB,AC,BC上,且DF∥BC,EF∥AB,若AD=2BD,则$\frac{CE}{BE}$的值为$\frac{1}{2}$.