题目内容
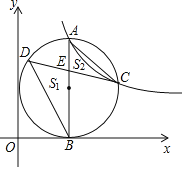
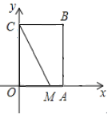
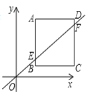
【题目】如图，在平面直角坐标系中，点
，四边形
是正方形，作直线
与正方形
边所在直线相交于
（1）若直线经过点
，求
的值；
（2）若直线平分正方形的面积，求
的坐标；
（3）若
的外心在其内部，直接写出的取值范围．
【答案】（1）
；（2）
；（3）
【解析】
（1）由
得
，进而得
，根据待定系数法，即可得到答案；
（2）设正方形的中心为
，过点作
轴于
，作
轴于
，从而求出点P的坐标，进而求出过点P的直线解析式：
，即可得到答案；
（3）由
的外心在其内部，得为锐角三角形．求出当直线
经过点
时所对应的k值，进而即可得到答案．
（1）
，
，
四边形
是正方形，
，
，
将代入
得：
，
；
（2）当直线经过正方形的中心时，平分正方形的面积．
过点作轴于，作轴于，
易得：
，
，
直线经过点，
，
∴
，
，
将
的横坐标
代入得：
，
；
（3）
的外心在其内部，
为锐角三角形．
当直线经过点时，为直角三角形，
由（1）可知：
，此时，
，
当时，为锐角三角形，
即的外心在其内部，
的取值范围为：．
练习册系列答案
教材全解字词句篇系列答案
相关题目
