题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
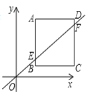
轴交于点![]() ,如图,作正方形
,如图,作正方形![]() ,点
,点![]() 在直线
在直线![]() 上,点
上,点![]() 在
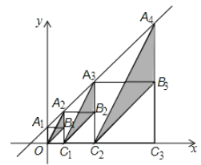
在![]() 轴上,将图中阴影部分三角形的面积从左到右依次记为
轴上,将图中阴影部分三角形的面积从左到右依次记为![]() ,则
,则
(1)![]() 的值为___________;
的值为___________;
(2)![]() 的值为___________.(含
的值为___________.(含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
【答案】![]()
![]()
【解析】
结合正方形的性质结合直线的解析式可得出:A2B1=OC1,A3B2=C1C2,A4B3=C2C3,…,结合三角形的面积公式即可得出:![]() ,
,![]() ,
,![]() ,…,根据面积的变化可找出变化规律
,…,根据面积的变化可找出变化规律![]() (n为正整数),依此规律即可得出结论.
(n为正整数),依此规律即可得出结论.
解:令一次函数![]() 中
中![]() ,则
,则![]() ,
,
∴点A1的坐标为(0,2),OA1=2.
∵四边形AnBnCnCn-1(n为正整数)均为正方形,
∴OA1=A1B1= B1C1=OC1=2,
令一次函数![]() 中x=2,则y=4,
中x=2,则y=4,
即A2C1=4,
∴A2B1=A2C1- B1C1=4-2=2=A1B1,
∴tan∠A2A1B1=1,
∵AnCn-1⊥x轴,
∴tan∠An+1AnBn=1.
∴A2B1=OC1,A3B2=C1C2,A4B3=C2C3,…,
∴![]() ,
,
∴![]() ,
,![]() ,…,
,…,
∴![]() ,
,![]() (n为正整数),
(n为正整数),
故答案为:(1)![]() ;(2)
;(2)![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目