Question

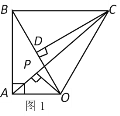
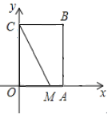
【题目】定义：如果一个三角形有一边上的中线等于这条边的一半，那么称三角形为“智慧三角形”．如图，在平面直角坐标系中，矩形的边，点，在边存在点，使得为“智慧三角形”，则点的坐标为：______．

Answer 1

【答案】或或

【解析】

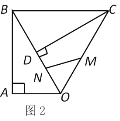
由题可知，“智慧三角形”是直角三角形，因为不确定哪个角是直角，所以分情况讨论，∠CPM=90°或∠CMP=90°，设设点P(3,a)，则AP=a，BP=4-a，根据勾股定理求出CP2，MP2，CM2，根据∠CPM=90°或∠CMP=90°，可以得到这三条边的关系，解之即可.

解：由题可知，“智慧三角形”是直角三角形，∠CPM=90°或∠CMP=90°

设点P(3,a)，则AP=a，BP=4-a

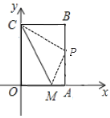
①若∠CPM=90°，在Rt△BCP中，

在Rt△MPA中，

在Rt△MCP中，

又∵

∴2a2-8a+26=20

即(a-3)(a-1)=0

解得a=3或a=1

∴P(3,3)或(3,1)

②若∠CMP=90°，在Rt△BCP中

在Rt△MPA中，

∵

在Rt△MCP中，

即

∴

综上，或(3,1)或(3,3)

故答案为或(3,1)或(3,3).