题目内容
5.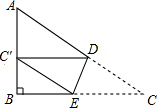 如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边的C′处,并且C′D∥BC,则CD的长是$\frac{40}{9}$.
如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边的C′处,并且C′D∥BC,则CD的长是$\frac{40}{9}$.
分析 先判定四边形C′DCE是菱形,再根据菱形的性质计算.
解答 解:设CD=x,
根据C′D∥BC,且有C′D=EC,
可得四边形C′DCE是菱形;
即Rt△ABC中,
AC=$\sqrt{{6}^{2}+{8}^{2}}$=10
$\frac{BE}{8}=\frac{{C}^{′}E}{10}=\frac{CD}{10}=\frac{x}{10}$,
EB=$\frac{4}{5}$x;
故可得BC=x+$\frac{4}{5}$x=8;
解得x=$\frac{40}{9}$.
故答案为:$\frac{40}{9}$.
点评 本题通过折叠变换考查学生的逻辑思维能力,解决此类问题,应结合题意,最好实际操作图形的折叠,易于找到图形间的关系.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
15.下列计算错误的是( )
| A. | 0.25°=900″ | B. | 1.5°=90′ | C. | 1000″=($\frac{5}{18}$)° | D. | 125.45°=1254.5′ |
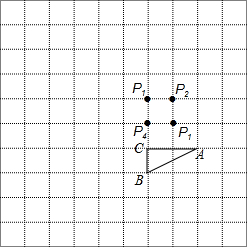 如图,在10×10的小正方形网格中,△ABC的顶点A、B、C在网格点上,P1、P2、P3、P4是其中一个小正方形的四个格点,将△ABC绕A点逆时针旋转90°,再向下平移2个单位,得到△A′B′C′;将△ABC按一定的规律顺次旋转,第一次将△ABC绕点P1逆时针旋转90°得到△A1B1C1;第二次将△A1B1C1绕点P2逆时针旋转90°得到△A2B2C2;第三次将△A2B2C2绕点P3逆时针旋转90°得到△A3B3C3,依次按旋转中心为P1、P2、P3、P4、P1、P2…旋转下去.
如图,在10×10的小正方形网格中,△ABC的顶点A、B、C在网格点上,P1、P2、P3、P4是其中一个小正方形的四个格点,将△ABC绕A点逆时针旋转90°,再向下平移2个单位,得到△A′B′C′;将△ABC按一定的规律顺次旋转,第一次将△ABC绕点P1逆时针旋转90°得到△A1B1C1;第二次将△A1B1C1绕点P2逆时针旋转90°得到△A2B2C2;第三次将△A2B2C2绕点P3逆时针旋转90°得到△A3B3C3,依次按旋转中心为P1、P2、P3、P4、P1、P2…旋转下去.
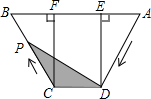 如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,垂足分别为E、F,且AE=EF=FB=5,DE=12,动点P从点C出发,沿C→B→A→D的方向以每秒1个单位长度的速度运动到点D停止,设运动时间为t秒,y=S△CDP,则y与t之间的函数图象大致是( )
如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,垂足分别为E、F,且AE=EF=FB=5,DE=12,动点P从点C出发,沿C→B→A→D的方向以每秒1个单位长度的速度运动到点D停止,设运动时间为t秒,y=S△CDP,则y与t之间的函数图象大致是( )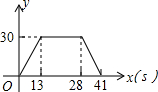

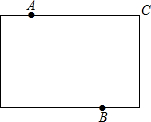 某地拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉P到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示.请利用尺规作图作出音乐喷泉P的位置.(要求:不写作法,但要保留作图痕迹,必须用铅笔作图).
某地拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉P到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示.请利用尺规作图作出音乐喷泉P的位置.(要求:不写作法,但要保留作图痕迹,必须用铅笔作图).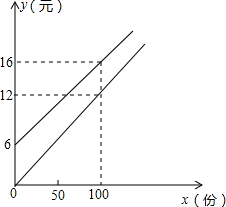 某校实施“学讲计划”教学,需印制若干份自主导学单,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷分数x(份)之间的函数关系如图所示:
某校实施“学讲计划”教学,需印制若干份自主导学单,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷分数x(份)之间的函数关系如图所示: