题目内容
12. 如图,AB是圆O的直径,DB,DC分别切圆O于点B,C,若∠ACE=25°,则∠D的度数是( )
如图,AB是圆O的直径,DB,DC分别切圆O于点B,C,若∠ACE=25°,则∠D的度数是( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
分析 连接BC,由弦切角定理得∠ACE=∠ABC,再由切线的性质求得∠DBC,最后由切线长定理求得∠D的度数.
解答 解:连接BC,
∵DB、DE分别切⊙O于点B、C,
∴∠ACE=∠ABC,BD=DC,
∵∠ACE=25°,
∴∠ABC=25°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠DBC=∠DCB=90°-25°=65°,
∴∠D=50°.
故选A.
点评 本题考查了切线的性质、圆周角定理、弦切角定理等知识,综合性强,难度中等,熟记和圆有关的各种性质定理是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
3.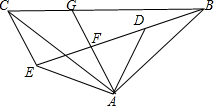 如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,所给结论:①∠BAD=∠CAE;②tan∠ABE=$\frac{\sqrt{3}}{3}$;③AG∥CE;④2AF+CE=BE;⑤AD=CG中,正确的有( )
如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,所给结论:①∠BAD=∠CAE;②tan∠ABE=$\frac{\sqrt{3}}{3}$;③AG∥CE;④2AF+CE=BE;⑤AD=CG中,正确的有( )
 如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,所给结论:①∠BAD=∠CAE;②tan∠ABE=$\frac{\sqrt{3}}{3}$;③AG∥CE;④2AF+CE=BE;⑤AD=CG中,正确的有( )
如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,所给结论:①∠BAD=∠CAE;②tan∠ABE=$\frac{\sqrt{3}}{3}$;③AG∥CE;④2AF+CE=BE;⑤AD=CG中,正确的有( )| A. | ①③⑤ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
20.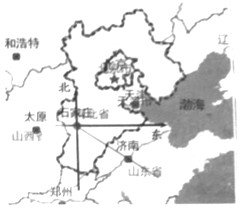 如图,济南大约位于石家庄的南偏东56°方向上,则石家庄大约位于济南的( )
如图,济南大约位于石家庄的南偏东56°方向上,则石家庄大约位于济南的( )
 如图,济南大约位于石家庄的南偏东56°方向上,则石家庄大约位于济南的( )
如图,济南大约位于石家庄的南偏东56°方向上,则石家庄大约位于济南的( )| A. | 北偏西56°方向上 | B. | 北偏西34°方向上 | C. | 南偏西34°方向上 | D. | 南偏东56°方向上 |
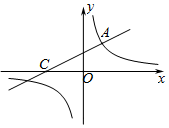 如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C.
如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C.



 如图,在△ABC中,AB=AC,∠A=36°,线段AB的垂直平分线MN分别交AB、AC于N、M.
如图,在△ABC中,AB=AC,∠A=36°,线段AB的垂直平分线MN分别交AB、AC于N、M.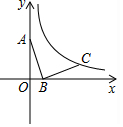 如图,在平面直角坐标系中,点A、B的坐标分贝为(0,3)、(1,0),将线段AB绕点B顺时针旋转90°,得到线段BC,若点C落在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为( )
如图,在平面直角坐标系中,点A、B的坐标分贝为(0,3)、(1,0),将线段AB绕点B顺时针旋转90°,得到线段BC,若点C落在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为( )