题目内容
17.解不等式:|x+5|-|2x-1|>2-x.分析 先分三种情况:当x<-5时;然后解不等式,当-5≤x<$\frac{1}{2}$时;当x≥$\frac{1}{2}$时,进行绝对值的化简,然后解不等式.
解答 解:当x<-5时,-x-5+2x-1>2-x,
解得:x>4,
此时无解;
当-5≤x<$\frac{1}{2}$时,x+5+2x-1>2-x,
解得:x>-$\frac{1}{2}$,
则不等式的解集为:-$\frac{1}{2}$<x<$\frac{1}{2}$;
当x≥$\frac{1}{2}$时,x+5-2x+1>2-x,
此时无解.
故不等式的解集为:-$\frac{1}{2}$<x<$\frac{1}{2}$.
点评 本题考查了解简单不等式的能力,解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
相关题目
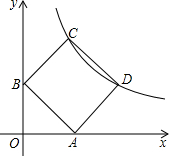 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$的图象两点C、D,以CD为边作正方形ABCD,点A、B分别在x轴、y轴的正半轴上,点B坐标为(0,1)且∠ABO=45°.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$的图象两点C、D,以CD为边作正方形ABCD,点A、B分别在x轴、y轴的正半轴上,点B坐标为(0,1)且∠ABO=45°.