题目内容
7.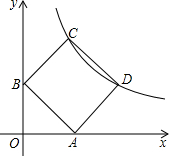 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$的图象两点C、D,以CD为边作正方形ABCD,点A、B分别在x轴、y轴的正半轴上,点B坐标为(0,1)且∠ABO=45°.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$的图象两点C、D,以CD为边作正方形ABCD,点A、B分别在x轴、y轴的正半轴上,点B坐标为(0,1)且∠ABO=45°.(1)求k的值;
(2)求CD所在直线的解析式.
分析 (1)作ED⊥x轴,判断出△BAE≌△DAE,求出DE和AE的长,得到D点坐标,求出k的值;
(2)求出AB的解析式,从而得到直线CD的比例系数,将D代入解析式,求出g的值,从而得到直线CD的解析式.
解答 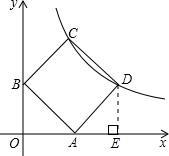 解:(1)作ED⊥x轴,
解:(1)作ED⊥x轴,
∵∠ABO=45°,
∴∠BAO=45°,
则∠DAE=90°-45°=45°,
在Rt△BAE和Rt△DAE中,
$\left\{\begin{array}{l}∠BOA=∠AED\\∠BAO=∠DAE\\ BA=AD\end{array}\right.$,
∴△BAE≌△DAE(AAS),
∴OB=OA=AE=DE=1,
∴OE=1+1=2,DE=1,
∴D点坐标为(2,1),
k=2×1=2;
(2)设AB解析式为y=mx+n,
将A(1,0)和B(0,1)分别代入解析式得,$\left\{\begin{array}{l}m+n=0\\ n=1\end{array}\right.$,
解得,$\left\{\begin{array}{l}m=-1\\ n=1\end{array}\right.$,函数解析式为y=-x+1;
∵AB∥CD,
设CD解析式为y=-x+g,
将D(2,1)代入解析式得g=3,
直线CD解析式为y=-x+3.
点评 本题考查了反比例函数解析式,熟悉反比例函数的性质、全等三角形的判定、待定系数法求函数解析式是解题的关键.

练习册系列答案
相关题目
 如图2、图3,AB∥EF,∠D与∠B,∠EFD有何数量关系?
如图2、图3,AB∥EF,∠D与∠B,∠EFD有何数量关系? 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,m+1)和CD边上的点E的纵坐标为$\frac{2}{3}$,过点E的直线l交于x轴于点F,交y轴于点G(0,-2),则OB:BF:FC为( )
如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,m+1)和CD边上的点E的纵坐标为$\frac{2}{3}$,过点E的直线l交于x轴于点F,交y轴于点G(0,-2),则OB:BF:FC为( )