题目内容
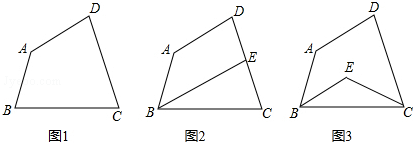
10.四边形ABCD中,∠A=145°,∠D=75°.(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
分析 (1)根据四边形的内角和即可得到结论;
(2)根据平行线的性质得到∠ABE=35°,∠BED=105°,由∠ABC的角平分线BE交DC于点E,得到∠CBE=∠ABE=35°,根据三角形的外角的性质即可得到结论;
(3)根据四边形的性质得到∠ABC+∠BCD=140°,根据三角形的内角和即可得到结论.
解答 解:(1)∵∠A=145°,∠D=75°,
∴∠B=∠C=$\frac{1}{2}$(360°-145°-75°)=70°;
(2)∵BE∥AD,∠A=145°,∠D=75°,
∴∠ABE=180°-∠A=35°,∠BED=180°-∠D=105°,
∵∠ABC的角平分线BE交DC于点E,
∴∠CBE=∠ABE=35°,
∴∠C=∠BED-∠EBC=70°;
(3)∵∠A=145°,∠D=75°,
∴∠ABC+∠BCD=360°-∠A-∠C=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=$\frac{1}{2}$(∠ABC+∠DCB)=70°,
∴∠BEC=110°.
点评 本题主要考查了三角形的内角和,多边形的内角和定理等知识点的理解和掌握,能求出∠ABC+∠DCB的度数是解此题的关键.

练习册系列答案
相关题目
20.二次函数y=-2(x-4)2-5的开口方向、对称轴分别是( )
| A. | 开口向上、直线x=-4 | B. | 开口向上、直线x=4 | ||
| C. | 开口向下、直线x=-4 | D. | 开口向下、直线x=4 |
18.下列运算正确的是( )
| A. | a2+a3=a5 | B. | (-2a3)2=4a6 | C. | a6÷a3=a2 | D. | (a+2b)2=a2+2ab+b2 |

 如图已知△ABC,请你用三角尺和量角器作图,作△ABC的:①中线AD;②角平分线BE;③高CH.
如图已知△ABC,请你用三角尺和量角器作图,作△ABC的:①中线AD;②角平分线BE;③高CH.


