题目内容
17.如图a,已知长方形纸带ABCD,AB∥CD,AD∥BC,∠BFE=70°,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b.(1)图a中,∠AEG=40°;
(2)图a中,∠BMG=50°;
(3)图b中,∠EFN=30°.
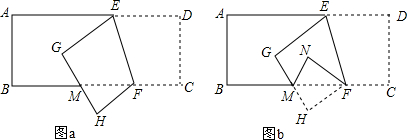
分析 (1)先根据∠BFE=70°求出∠HFM的度数,进可得出∠EFC的度数,根据平行线的性质求出∠DEF的度数,由平角的定义即可得出结论;
(2)由(1)知,∠HFM=40°,再由翻折变换的性质得出∠H=∠C=90°,由三角形内角和定理得出∠HMF的度数,根据对顶角相等即可得出结论;
(3)先根据图形翻折变换的性质得出∠MFN=∠HFM=40°,再由∠BFE=70°即可得出结论.
解答 解:(1)∵∠BFE=70°,
∴∠HFM=180°-140°=40°.
∴∠EFC=70°+40°=110°.
∵AD∥BC,
∴∠DEF=180°-110°=70°,
∴∠GEF=∠DEF=70°,
∴∠AEG=180°-70°-70°=40°.
故答案为:40;
(2)∵由(1)知,∠HFM=40°,∠H=∠C=90°,
∴∠HMF=90°-40°=50°.
∵∠HMF与∠BMG是对顶角,
∴∠BMG=∠HMF=50°.
故答案为:50;
(3)∵△MNF由△MHF翻折而成,
∴∠MFN=∠HFM=40°,
∵∠BFE=70°,
∴∠EFN=∠BFE-∠MFN=70°-40°=30°.
故答案为:30.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
15.下列几何体中,主视图、左视图、俯视图完全相同的是( )
| A. | 球 | B. | 圆锥 | C. | 圆柱 | D. | 长方体 |
16.抛物线y=x2-2x+m(m>0)与x轴分别交于点A(x1,0),B(x2,0),点A在点B的左侧,当x=x2-2时,则y的值的取值范围是( )
| A. | y<0 | B. | y≤0 | C. | y>m | D. | y≥m |
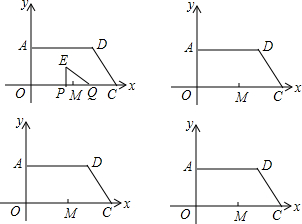
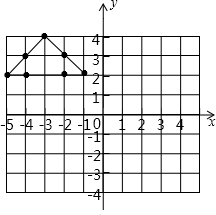 如图所示,将图中的点(-5,2),(-3,4),(-1,2),(-4,2),(-2,2),(-2,3),(-4,3)做如下变化:
如图所示,将图中的点(-5,2),(-3,4),(-1,2),(-4,2),(-2,2),(-2,3),(-4,3)做如下变化: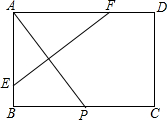 如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点.现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E,F.
如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点.现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E,F. 如图,在?ABCD中,CE平分∠BCD交AD边于点E,且AD=5,CD=3,则AE长为2.
如图,在?ABCD中,CE平分∠BCD交AD边于点E,且AD=5,CD=3,则AE长为2.