题目内容
5.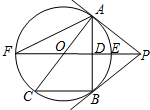 如图,PB为⊙O的切线,点B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF,
如图,PB为⊙O的切线,点B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF,(1)求证:直线PA为⊙O的切线,
(2)试探究线段EF,OD,OP之间的数量关系,并加以证明,
(3)若BC=6,tan∠F=$\frac{1}{2}$,求cos∠ACB的值和线段PE的长.
分析 (1)连接OB,先由切线的性质得出∠OBP=90°,再证明△OPA≌△OPB,由对应角相等广昌出∠OAP=∠OBP=90°,即可得出结论;
(2)证△OAD∽△OPA,得出对应边成比例$\frac{OA}{OP}=\frac{OD}{OA}$,即OA2=OD•OP,再由EF=2OA,即可得出结论;
(3)连接AE,由已知条件设AE=x,AF=2x,根据勾股定理得出EF,由面积得出AD,根据勾股定理得出方程,解方程求出x,即可求出cos∠ACB的值,再求出OD、OP的长,即可求出线段PE的长.
解答 (1)证明:连接OB,如图所示: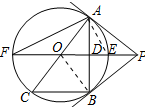 ∵OP⊥AB,
∵OP⊥AB,
∴OP平分AB,
∴OP是AB的垂直平分线,
∴PA=PB,
∵PB为⊙O的切线,
∴OB⊥PB,
∴∠OBP=90°,
在△OPA和△OPB中,$\left\{\begin{array}{l}{OA=OB}&{\;}\\{PA=PB}&{\;}\\{OP=OP}&{\;}\end{array}\right.$,
∴△OPA≌△OPB(SSS),
∴∠OAP=∠OBP=90°,
∴直线PA为⊙O的切线;
(2)EF2=4OD•OP;
理由:∵∠OAP=∠ADO=90°,∠AOD=∠POA,
∴△OAD∽△OPA,
∴$\frac{OA}{OP}=\frac{OD}{OA}$,即OA2=OD•OP,
∵EF为圆的直径,
∴EF=2OA,
∴$\frac{1}{4}$EF2=OD•OP,
即EF2=4OD•OP;
(3)连接AE,如图所示:
∵EF为直径,
∴∠FAE=90°.
∵tan∠F=$\frac{1}{2}$,
∴$\frac{AE}{AF}$=$\frac{1}{2}$,
∴设AE=x,AF=2x,
则由勾股定理,得
EF=$\sqrt{A{E}^{2}+A{F}^{2}}$=$\sqrt{5}$x,
∵$\frac{1}{2}$AE•AF=$\frac{1}{2}$EF•AD,
∴AD=$\frac{2\sqrt{5}}{5}$x.
又∵AB⊥EF,
∴AB=2AD=$\frac{4\sqrt{5}}{5}x$,
∴Rt△ABC中,AC=$\sqrt{5}$x,BC2+AB2=AC2,
∴62+($\frac{4\sqrt{5}}{5}$x)2=($\sqrt{5}$x)2,
解得:x=2$\sqrt{5}$,
∴AC=$\sqrt{5}$•2$\sqrt{5}$=10,
∴cos∠ACB=$\frac{BC}{AC}$=$\frac{6}{10}$=$\frac{3}{5}$;
∵AD═$\frac{2\sqrt{5}}{5}$×2$\sqrt{5}$=4,OA=$\frac{1}{2}$AC=5,
∴OD=$\sqrt{{5}^{2}-{4}^{2}}$=3,
又∵OA2=OD•OP,
∴OP=$\frac{O{A}^{2}}{OD}$=$\frac{{5}^{2}}{3}$=$\frac{25}{3}$,
∴PE=OP-OE=$\frac{25}{3}$-5=$\frac{10}{3}$.
点评 本题考查了切线的判定与性质、相似三角形的判定与性质、勾股定理、锐角三角函数;本题综合性强,难度较大,特别是(3)中,通过设未知数,根据勾股定理列出方程,解方程以达到求解的目的.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案 如图,由B到A的方向是( )
如图,由B到A的方向是( )| A. | 南偏东30° | B. | 东偏南60° | C. | 西偏北30° | D. | 北偏西60° |
| A. | -1<x<0 | B. | -2<x<-1 | C. | 0<x<3 | D. | 3<x<4 |
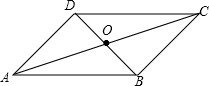 如图,在?ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△AOB的周长为( )
如图,在?ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△AOB的周长为( )| A. | 32 | B. | 24 | C. | 21 | D. | 18 |
| A. | 0•a不是单项式 | B. | -$\frac{xyz}{3}$的系数是-$\frac{1}{3}$ | ||
| C. | -$\frac{abc}{4}$的系数是-4 | D. | x3y的系数是0 |
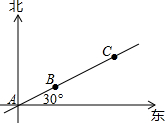 如图,A,B,C三人的位置在同一直线上,AB=5米,BC=10米,下列说法正确的是( )
如图,A,B,C三人的位置在同一直线上,AB=5米,BC=10米,下列说法正确的是( )| A. | C在A的北偏东30°方向的15米处 | B. | A在C的北偏东60°方向的15米处 | ||
| C. | C在B的北偏东60°方向的10米处 | D. | B在A的北偏东30°方向的5米处 |
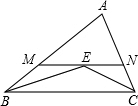 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=15,则线段MN的长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=15,则线段MN的长为( )