题目内容
5. 如图,在梯形ABCD中,AB∥DC,∠BCD=90°,且AB=2,BC=3,tan∠ADC=3.
如图,在梯形ABCD中,AB∥DC,∠BCD=90°,且AB=2,BC=3,tan∠ADC=3.(1)求证:DC=BC;
(2)E是梯形内的一点,F是梯形外的一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论.
分析 (1)过A作DC的垂线AM交DC于M,可得四边形ABCM是矩形,根据矩形的对边相等求出AM=3,再根据tan∠ADC=3求出DM=1,然后求出CD=3,从而得证;
(2)利用“边角边”证明△DEC和△BFC全等,根据全等三角形对应边相等可得CE=CF,全等三角形对应角相等可得∠ECD=∠BCF,然后求出∠ECF=90°,从而判断出是等腰直角三角形.
解答 (1)证明:过A作DC的垂线AM交DC于M,
则四边形ABCM是矩形,
则AM=BC=3,MC=AB=2,
又∵tan∠ADC=$\frac{AM}{DM}$=3,
∴DM=1,
∴DC=DM+MC=3,
∴DC=BC;
(2)解:△ECF是等腰直角三角形.理由如下:
∵在△DEC和△BFC中,
$\left\{\begin{array}{l}{DE=BF}\\{∠EDC=∠FBC}\\{DC=BC}\end{array}\right.$,
∴△DEC≌△BFC(SAS),
∴CE=CF,∠ECD=∠BCF,
∴∠ECF=∠BCF+∠BCE=∠ECD+∠BCE=∠BCD=90°,
即△ECF为等腰直角三角形.
点评 本题考查了梯形的性质,全等三角形的判定与性质,等腰直角三角形的判定,解直角三角形,准确识图确定出全等三角形是解题的关键.

练习册系列答案
相关题目
18.要使二次根式$\sqrt{2x-4}$在实数范围内有意义,则x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x<2 | D. | x=2 |
16.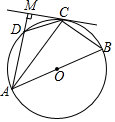 如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
 如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )| A. | 20° | B. | 35° | C. | 40° | D. | 55° |
 某同学在体育训练中统计了自己五次“1分钟跳绳”成绩,并绘制了如图所示的折线统计图,这五次“1分钟跳绳”成绩的中位数是183个.
某同学在体育训练中统计了自己五次“1分钟跳绳”成绩,并绘制了如图所示的折线统计图,这五次“1分钟跳绳”成绩的中位数是183个. 如图,是将抛物线y=-x2平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C.
如图,是将抛物线y=-x2平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C.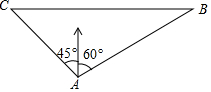 一艘轮船在小岛A的北偏东60°距小岛80海里的B处,沿正西方向航行2小时后到达小岛的北偏西45°的C处,则该船行驶的速度为20+20$\sqrt{3}$海里/小时.
一艘轮船在小岛A的北偏东60°距小岛80海里的B处,沿正西方向航行2小时后到达小岛的北偏西45°的C处,则该船行驶的速度为20+20$\sqrt{3}$海里/小时.