题目内容
16．
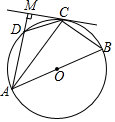如图，圆内接四边形ABCD的边AB过圆心O，过点C的切线与边AD所在直线垂直于点M，若∠ABC=55°，则∠ACD等于（ ）| A． | 20° | B． | 35° | C． | 40° | D． | 55° |
分析 由圆内接四边形的性质求出∠ADC=180°-∠ABC=125°，由圆周角定理求出∠ACB=90°，得出∠BAC=35°，由弦切角定理得出∠MCA=∠ABC=55°，由三角形的外角性质得出∠DCM=∠ADC-∠AMC=35°，即可求出∠ACD的度数．
解答 解：∵圆内接四边形ABCD的边AB过圆心O，
∴∠ADC+∠ABC=180°，∠ACB=90°，
∴∠ADC=180°-∠ABC=125°，∠BAC=90°-∠ABC=35°，
∵过点C的切线与边AD所在直线垂直于点M，
∴∠MCA=∠ABC=55°，∠AMC=90°，
∵∠ADC=∠AMC+∠DCM，
∴∠DCM=∠ADC-∠AMC=35°，
∴∠ACD=∠MCA-∠DCM=55°-35°=20°；
故选：A．
点评 本题考查了圆内接四边形的性质、圆周角定理、三角形的外角性质、弦切角定理等知识；熟练掌握圆内接四边形的性质和圆周角定理是解决问题的关键．
练习册系列答案
相关题目
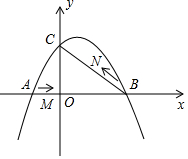如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）与y轴交与点C（0，3），与x轴交于A、B两点，点B坐标为（4，0），抛物线的对称轴方程为x=1．
4．下列四个数：-3，-$\sqrt{3}$，-π，-1，其中最小的数是（ ）
| A． | -π | B． | -3 | C． | -1 | D． | -$\sqrt{3}$ |
如图，在平面直角坐标系中，Rt△AOB的斜边OA在x轴的正半轴上，∠OBA=90°，且tan∠AOB=$\frac{1}{2}$，OB=2$\sqrt{5}$，反比例函数y=$\frac{k}{x}$的图象经过点B．
如图，在梯形ABCD中，AB∥DC，∠BCD=90°，且AB=2，BC=3，tan∠ADC=3．
