题目内容
若抛物线y=x2+bx+c与x轴的两个交点坐标分别为(2,0)(4,0),则抛物线的对称轴是 .
考点:抛物线与x轴的交点,二次函数图象上点的坐标特征
专题:计算题
分析:将(2,0)与(4,0)代入抛物线y=x2+bx+c,列出方程组求出b,c,再根据对称轴x=-
得出答案.
| b |
| 2a |
解答:解:∵抛物线y=x2+bx+c与x轴的两个交点坐标分别为(2,0)(4,0),
∴
,
解得
,
∴抛物线的解析式为y=x2-6x+8,
∴对称轴为x=3,
故答案为x=3.
∴
|
解得
|
∴抛物线的解析式为y=x2-6x+8,
∴对称轴为x=3,
故答案为x=3.
点评:本题考查了抛物线与x轴的交点问题,二次函数图象上点的坐标特征,是基础知识要熟练掌握.

练习册系列答案
相关题目
下列图形中,既是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
如果满足|
-5|=a的实数x恰有6个值,那么a的取值范围是( )
| (x2-3x+2)2 |
| A、a≥-5 | ||
B、
| ||
C、5<a<
| ||
| D、0≤a≤5 |
 如图所示,在平面直角坐标系中,0为坐标原点,⊙E过点O.与x轴、y轴分别交于B、A两点,点E坐标为(-2,2
如图所示,在平面直角坐标系中,0为坐标原点,⊙E过点O.与x轴、y轴分别交于B、A两点,点E坐标为(-2,2 如图,BC=45,AC=21,△ABC被分成9个面积相等的小三角形,则DI+FK=
如图,BC=45,AC=21,△ABC被分成9个面积相等的小三角形,则DI+FK=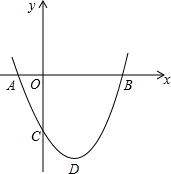 如图,二次函数y=ax2+bx+c(a>0).图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1、3,与y轴负半轴交于点C.下面五个结论:①2a+b=0;②a+b+c>0;③当x≤1时,y随x值的增大而增大;④当-1≤x≤3时,ax2+bx+c<0;⑤只有当a=
如图,二次函数y=ax2+bx+c(a>0).图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1、3,与y轴负半轴交于点C.下面五个结论:①2a+b=0;②a+b+c>0;③当x≤1时,y随x值的增大而增大;④当-1≤x≤3时,ax2+bx+c<0;⑤只有当a=