题目内容
14.计算:(1)2$\sqrt{18}$$-4\sqrt{\frac{1}{8}}$$+3\sqrt{32}$.
(2)($\sqrt{32}$$-2\sqrt{\frac{1}{3}}$)-($\sqrt{\frac{1}{8}}$$-\sqrt{75}$)
(3)($\sqrt{\frac{8}{27}}$$-5\sqrt{3}$)×$\sqrt{6}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后去括号合并即可;
(3)根据二次根式的乘法法则运算.
解答 解:(1)原式=6$\sqrt{2}$-$\sqrt{2}$+12$\sqrt{2}$
=17$\sqrt{2}$;
(2)原式=4$\sqrt{2}$-$\frac{2\sqrt{3}}{3}$-$\frac{\sqrt{2}}{4}$+5$\sqrt{3}$
=$\frac{15\sqrt{2}}{4}$+$\frac{13\sqrt{3}}{3}$;
(3)原式=$\sqrt{\frac{8}{27}×6}$-5$\sqrt{3×6}$
=$\frac{4}{3}$-15$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
4.下列命题是真命题的是( )
| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 对角线相等且互相垂直的四边形是正方形 | |
| C. | 平分弦的直径垂直于弦,并且平分弦所对的弧 | |
| D. | 三角形任意两边之差小于第三边 |
9.任何数与零相加,结果( )
| A. | 等于这个数的相反数 | B. | 等于零 | ||
| C. | 等于这个数本身 | D. | 为负数 |
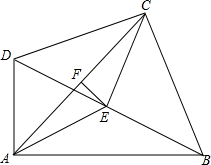 如图,在四边形ABCD中,∠DCB=∠DAB=Rt∠,点E是对角线BD的中点.
如图,在四边形ABCD中,∠DCB=∠DAB=Rt∠,点E是对角线BD的中点. 某种细胞经过30分钟由1个分裂成2个.
某种细胞经过30分钟由1个分裂成2个.