题目内容
15.(1)在下面的横线上填(“<”“>”或“=”).∵$\sqrt{3}-\sqrt{2}$=$\frac{1}{\sqrt{3}+\sqrt{2}}$,$\sqrt{2}-\sqrt{1}$=$\frac{1}{\sqrt{2}+\sqrt{1}}$,∴$\sqrt{3}-\sqrt{2}$<$\sqrt{2}-\sqrt{1}$.
∵$\sqrt{4}-\sqrt{3}$=$\frac{1}{\sqrt{4}+\sqrt{3}}$,$\sqrt{3}-\sqrt{2}=\frac{1}{\sqrt{3}+\sqrt{2}}$,∴$\sqrt{4}-\sqrt{3}$<$\sqrt{3}-\sqrt{2}$.
(2)请你猜想$\sqrt{n+1}-\sqrt{n}$与$\sqrt{n}-\sqrt{n-1}$(n大于1的整数)的大小关系,并加以证明.
分析 (1)根据分子相同时,分母越大,这个数越小进行判断即可;
(2)根据例题进行计算即可.
解答 解:(1)∵分子相同时,分母越大,这个数越小,
∴$\sqrt{3}-\sqrt{2}$<$\sqrt{2}-\sqrt{1}$;$\sqrt{4}-\sqrt{3}$<$\sqrt{3}-\sqrt{2}$.
(2)$\sqrt{n+1}-\sqrt{n}$<$\sqrt{n}-\sqrt{n-1}$
证明:$\sqrt{n+1}-\sqrt{n}$=$\frac{1}{\sqrt{n+1}+\sqrt{n}}$;$\sqrt{n}-\sqrt{n-1}$=$\frac{1}{\sqrt{n}+\sqrt{n-1}}$;
∵$\frac{1}{\sqrt{n+1}+\sqrt{n}}$$<\frac{1}{\sqrt{n}+\sqrt{n-1}}$,
∴$\sqrt{n+1}-\sqrt{n}$<$\sqrt{n}-\sqrt{n-1}$.
点评 本题主要考查的是比较实数的大小,明确分子相同时,分母越大,这个数越小是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
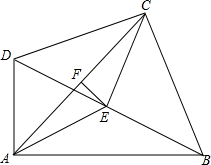 如图,在四边形ABCD中,∠DCB=∠DAB=Rt∠,点E是对角线BD的中点.
如图,在四边形ABCD中,∠DCB=∠DAB=Rt∠,点E是对角线BD的中点. 某种细胞经过30分钟由1个分裂成2个.
某种细胞经过30分钟由1个分裂成2个. 如图,图中两个正方形的边长分别是a,b.
如图,图中两个正方形的边长分别是a,b.