题目内容
19．若抛物线y=x2-4x+4-t（t为实数）在0＜x＜3的范围内与x轴有公共点，则t的取值范围为（ ）| A． | 0＜t＜4 | B． | 0≤t＜4 | C． | 0＜t＜1 | D． | t≥0 |
分析 先利用配方法得到抛物线的顶点为（2，-t），再分类讨论：当抛物线与x轴的公共点为顶点时，-t=0，解得t=0；当抛物线在0＜x＜3的范围内与x轴有公共点，如图，顶点在x轴下方，所以t＞0，当抛物线在原点与对称轴之间与x轴有交点时，x=0，y＞0，所以4-t＞0，解得t＜4；当抛物线在（3，0）与对称轴之间与x轴有交点时x=3，y＞0，即1-t＞0，解得t＜1，所以此时t的范围为0＜t＜4，综上两种情况即可得到t的范围为0≤t＜4．
解答 解：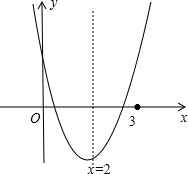
y=x2-4x+4-t=（x-2）2-t，
抛物线的顶点为（2，-t），
当抛物线与x轴的公共点为顶点时，-t=0，解得t=0，
当抛物线在0＜x＜3的范围内与x轴有公共点，如图，-t＜0，解得t＞0，则x=0时，y＞0，即4-t＞0，解得t＜4；x=3时，y＞0，即1-t＞0，解得t＜1，此时t的范围为0＜t＜4，
综上所述，t的范围为0≤t＜4．
故选B．
点评 本题考查了抛物线与x轴的交点：把求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标转化为解关于x的一元二次方程．运用数形结合的思想是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．某公司派出甲车前往某地完成任务，此时，有一辆流动加油车与他同时出发，且在同一条公路上匀速行驶（速度保持不变）．为了确定汽车的位置，我们用OX表示这条公路，原点O为零千米路标，并作如下约定：速度为正，表示汽车向数轴的正方向行驶；速度为负，表示汽车向数轴的负方向行驶；速度为零，表示汽车静止．行程为正，表示汽车位于零千米的右侧；行程为负，表示汽车位于零千米的左侧；行程为零，表示汽车位于零千米处．两车行程记录如表：
由上面表格中的数据，解决下列问题：
（1）甲车开出7小时时的位置为-90km，流动加油车出发位置为-80km；
（2）当两车同时开出x小时时，甲车位置为190-40xkm，流动加油车位置为-80+50x km （用x的代数式表示）；
（3）甲车出发前由于未加油，汽车启动后司机才发现油箱内汽油仅够行驶3小时，问：甲车连续行驶3小时后，能否立刻获得流动加油车的帮助？请说明理由．
| 时间（h） | 0 | 5 | 7 | x |
| 甲车位置（km） | 190 | -10 | ||
| 流动加油车位置（km） | 170 | 270 |
（1）甲车开出7小时时的位置为-90km，流动加油车出发位置为-80km；
（2）当两车同时开出x小时时，甲车位置为190-40xkm，流动加油车位置为-80+50x km （用x的代数式表示）；
（3）甲车出发前由于未加油，汽车启动后司机才发现油箱内汽油仅够行驶3小时，问：甲车连续行驶3小时后，能否立刻获得流动加油车的帮助？请说明理由．
在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2）．则正方形ABCD的面积为5，延长CB交x轴于点A1，作正方形A1B1C1C，则正方形A1B1C1C的面积为$\frac{45}{4}$；延长C1B1交x轴于点A2，作正方形A2B2C2C1，…按这样的规律进行下去，正方形A2015B2015C2015C2014的面积为5×${（{\frac{9}{4}}）^{2015}}$．
4．下列等式成立的是（ ）
| A． | （-$\frac{2}{3}$）-2=$\frac{4}{9}$ | B． | $\frac{-a+b}{c}$=-$\frac{a+b}{c}$ | ||
| C． | 0.00061=6.1×10-5 | D． | $\frac{-a-b}{-a+b}$=$\frac{a+b}{a-b}$ |
“中华人民共和国道路交通管理条例”规定：小汽车在城市街道上的行驶速度不得超过60千米/时．这时一辆小汽车在一条城市街道直路上行驶，某一时刻刚好行驶到路对面车速检测仪A正前方50米C处，过了8秒后，测得小汽车位置B与车速检测仪A之间的距离为130米，这辆小汽车超速了吗？请说明理由．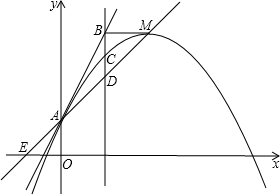
如图，无论非零的a取何值，抛物线y=ax2+bx+c的顶点M都在直线yAE=kx+1上（E、A分别在x轴、y轴上），且OA=OE．
如图，在△ABC中，BC=8cm，BP、CP分别是∠ABC和∠ACB的平分线，且PD∥AB，PE∥AC．