题目内容

10．多项式x2-8x+k可化为（x-a）2（其中a≠0）的形式，则k=16．

分析 根据完全平方公式的结构，按照要求x2-8x+k=x2-8x+16=（x-4）2，可知a=4，k=16．

解答 解：∵x2-8x+k=x2-8x+16=（x-4）2，
∴a=4，k=16．
故答案为16．

点评 本题主要考查完全平方公式的变形，熟记公式结构是解题的关键．完全平方公式：（a±b）2=a2±2ab+b2．

练习册系列答案
相关题目
19．计算：
（1）$\sqrt{18}$-$\frac{3}{\sqrt{2}}$+2$\sqrt{2}$
（2）$\frac{\sqrt{28}-\sqrt{14}}{\sqrt{7}}$．
20．某农场经过两年的时间将产量从200万斤提高到260万斤，其中第二年增产的百分率是第一年的2倍．设第一年增产的百分率为x，则可列方程为（　　）
A．200（1+x）（1+2x）=260B．200（1+2x）2=260
C．200（1+x）+200（1+2x）2=260D．200（1+x）2=260
17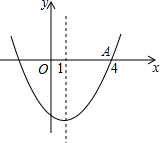．如图，二次函数y=ax2+bx+c图象的对称轴为直线x=1，若其与x轴的一个交点为A（4，0），则由图象可知，该二次函数与x轴的另一个交点坐标是（　　）
A．（-4，0）B．（-3，0）C．（-2，0）D．（-1，0）
5．计算
（1）23-17-（-7）+（_16）
（2）36×（$\frac{1}{9}$-$\frac{1}{6}$-$\frac{1}{18}$）
（3）-13-（1-0.5）×$\frac{1}{3}$×[2-（-3）2]
（4）16÷（-2）3-（-$\frac{1}{8}$）×（-4）+（-1）100．
15．$\frac{2}{3}$的倒数是$\frac{3}{2}$；-3.5的相反数为3.5；绝对值是3的数是±3．
2．计算
（1）-20+（-14）-（-18）-13　　   
（2）2+3×（-4）-（-2）2÷4
（3）（$\frac{2}{3}$+$\frac{3}{4}$-$\frac{5}{6}$）×（-12）
（4）（-2）3-$\frac{1}{3}$÷5×|1-（4）2|
19．若抛物线y=x2-4x+4-t（t为实数）在0＜x＜3的范围内与x轴有公共点，则t的取值范围为（　　）
A．0＜t＜4B．0≤t＜4C．0＜t＜1D．t≥0
20．一张桌子上摆放有若干个形状、大小完全相同的碟子，现从三个方向看，看到的图形如图所示，则这张桌子上碟子的总数可能是（　　）
A．11B．14C．18D．19

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网