题目内容
4. 如图,AB∥DC,增加折线条数,相应角的个数也会增多,∠B,∠E,∠F,∠G,∠D之间又会有何关系?
如图,AB∥DC,增加折线条数,相应角的个数也会增多,∠B,∠E,∠F,∠G,∠D之间又会有何关系?
分析 首先作EM∥AB,FN∥AB,GP∥AB,可得EM∥FN,FN∥GP,GP∥DC;然后根据平行线的性质,可得∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,据此判断出∠B+∠F+∠D=∠E+∠G即可.
解答 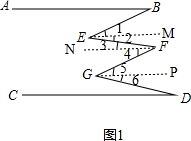 解:如图1,作EM∥AB,FN∥AB,GP∥AB,
解:如图1,作EM∥AB,FN∥AB,GP∥AB,
∵AB∥DC,
∴EM∥FN,FN∥GP,GP∥DC,
∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,
∴∠B+∠3+∠4+∠D=∠1+∠2+∠5+∠6,
∴∠B+∠F+∠D=∠E+∠G.
点评 此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等.

练习册系列答案
相关题目
13.下列命题是假命题的是( )
| A. | 对角线互相垂直且相等的平行四边形是正方形 | |
| B. | 对角线互相垂直的矩形是正方形 | |
| C. | 对角线相等的菱形是正方形 | |
| D. | 对角线互相垂直的四边形是正方形 |
 如图所示,A,B,C三点的坐标分别是A(-4,0),B(-$\sqrt{2}$,0),C(1,3).
如图所示,A,B,C三点的坐标分别是A(-4,0),B(-$\sqrt{2}$,0),C(1,3).
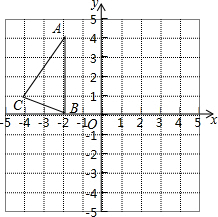 如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),将△ABC绕原点O旋转180度得到△A1B1C1.结合所给的平面直角坐标系解答下列问题:
如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),将△ABC绕原点O旋转180度得到△A1B1C1.结合所给的平面直角坐标系解答下列问题: 如图,AE是△ABC的外角平分线,∠B=∠C,试说明AE∥BC的理由.
如图,AE是△ABC的外角平分线,∠B=∠C,试说明AE∥BC的理由.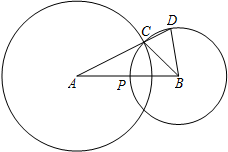 已知:如图,C是⊙A与⊙B的一个交点,联结AC,并延长交⊙B于点D,⊙B交AB于点P,联结BC、BD,AB=8,AC=6,⊙B的半径为x,线段AD的长为y.
已知:如图,C是⊙A与⊙B的一个交点,联结AC,并延长交⊙B于点D,⊙B交AB于点P,联结BC、BD,AB=8,AC=6,⊙B的半径为x,线段AD的长为y. 如图,图中的阴影部分表示什么数?你能写出3个符合要求的数吗?
如图,图中的阴影部分表示什么数?你能写出3个符合要求的数吗? 如图,△A′B′C′是由△ABC沿射线AC方向平移得到,若AC=5cm,A′C=2cm,则所平移的距离为3cm.
如图,△A′B′C′是由△ABC沿射线AC方向平移得到,若AC=5cm,A′C=2cm,则所平移的距离为3cm.