题目内容
8. 如图所示,A,B,C三点的坐标分别是A(-4,0),B(-$\sqrt{2}$,0),C(1,3).
如图所示,A,B,C三点的坐标分别是A(-4,0),B(-$\sqrt{2}$,0),C(1,3).(1)求△ABC的面积;($\sqrt{2}$≈1.414,结果保留一位小数)
(2)将△ABC向上平移2个单位长度,再往左平移1个单位长度得到△A′B′C′,请你画出平移后的图形,并分别写出A′,B′,C′三点的坐标.
分析 (1)把AB当作底边,C到AB的垂线段作为高,根据三角形的面积公式即可求出△ABC的面积;
(2)找到A、B、C向上平移2个单位长度,再往左平移1个单位长度后的对应点,顺次连接可得△A′B′C′,结合直角坐标系可得A′,B′,C′三点的坐标.
解答 解:(1)S△ABC=$\frac{1}{2}$(4-$\sqrt{2}$)×3=6-$\frac{3\sqrt{2}}{2}$≈6-1.5×1.414≈3.9;
(2)如下图,△A′B′C′即为平移后的图形.
A′(-5,2)、B′(-$\sqrt{2}$-1,2)、C′(0,5).
点评 本题考查了作图-平移变换,解答本题的关键是掌握平移的特点,根据平移规律找到各点平移变换后的位置.也考查了三角形的面积.

练习册系列答案
相关题目
20. 如图,因为AB∥CD,可以( )
如图,因为AB∥CD,可以( )
 如图,因为AB∥CD,可以( )
如图,因为AB∥CD,可以( )| A. | ∠1=∠2 | B. | ∠1=∠3 | C. | ∠1=∠4 | D. | ∠1=∠5 |
 如图直角坐标系中,A(-2,1),B(-3,-2),平移线段AB,使B点的对应点刚好与坐标原点O重合.
如图直角坐标系中,A(-2,1),B(-3,-2),平移线段AB,使B点的对应点刚好与坐标原点O重合.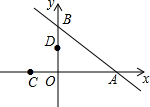 如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记得点C,折痕与y轴交于点D,则点D的坐标为(0,$\frac{4}{3}$).
如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记得点C,折痕与y轴交于点D,则点D的坐标为(0,$\frac{4}{3}$). 如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标为(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为(3,2$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标为(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为(3,2$\sqrt{3}$). 如图,AB∥DC,增加折线条数,相应角的个数也会增多,∠B,∠E,∠F,∠G,∠D之间又会有何关系?
如图,AB∥DC,增加折线条数,相应角的个数也会增多,∠B,∠E,∠F,∠G,∠D之间又会有何关系?