题目内容
12.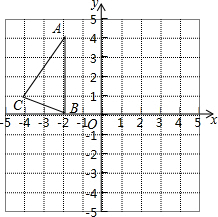 如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),将△ABC绕原点O旋转180度得到△A1B1C1.结合所给的平面直角坐标系解答下列问题:
如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),将△ABC绕原点O旋转180度得到△A1B1C1.结合所给的平面直角坐标系解答下列问题:(1)画出△A1B1C1;
(2)画出一个△A2B2C2,使它分别与△ABC,△A1B1C1轴对轴(其中点A,B,C与点A2,B2,C2对应);
(3)在(2)的条件下,若过点B的直线平分四边形ACC2A2的面积,请直接写出该直线的函数解析式.
分析 (1)首先由旋转的性质求得对应点的坐标,然后画出图形即可;
(2)由轴对称图形的性质找出对应点的坐标,然后画出图形即可;
(3)分别画出三角形关于x轴对称和关于y轴对称的图形,然后再找出过点B平分四边形面积的直线,最后求得解析式即可.
解答 解:(1)如图1所示: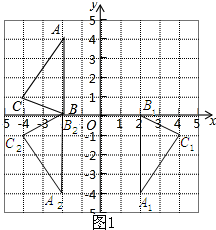
(2)如图1所示:直线解解析式为y=0;
如图2所示: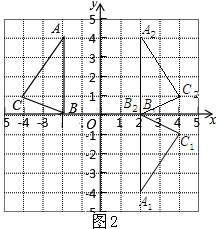
经过点B和(0,2.5)的直线平分四边形ACC2A2的面积,
设直线的解析式为y=kx+b,
将(-2,0)和(0,2.5)代入得:$\left\{\begin{array}{l}{b=\frac{5}{2}}\\{-2k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{5}{4}}\\{b=\frac{5}{2}}\end{array}\right.$
直线的解析式为y=$\frac{5}{4}x+\frac{5}{2}$.
综上所述:直线的解析式为y=0或y=$\frac{5}{4}x+\frac{5}{2}$.
点评 本题主要考查的是旋转变换、轴对称变换以及求一次函数的表达式,掌握旋转、轴对称的性质是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标为(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为(3,2$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标为(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为(3,2$\sqrt{3}$). 如图,反比例函数y=$\frac{k}{x}$与矩形OABC交于E、F两点,其中E为AB的中点,S△OBF=$\frac{9}{2}$,则k=-6.
如图,反比例函数y=$\frac{k}{x}$与矩形OABC交于E、F两点,其中E为AB的中点,S△OBF=$\frac{9}{2}$,则k=-6.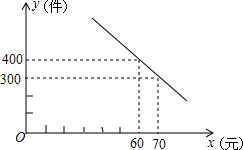 某服装厂销售一种成本为50元的衬衣,规定销售的单价不得低于成本价,又不能高于70元,销售量y(件)与销售单价x(元)的关系如图所示.
某服装厂销售一种成本为50元的衬衣,规定销售的单价不得低于成本价,又不能高于70元,销售量y(件)与销售单价x(元)的关系如图所示.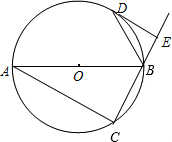 已知:如图,△ABC是⊙O的内角三角形,△ABC的外角平分线BD交⊙O于D,DE与⊙O相切,交CB的延长线于E.
已知:如图,△ABC是⊙O的内角三角形,△ABC的外角平分线BD交⊙O于D,DE与⊙O相切,交CB的延长线于E. 如图,AB∥DC,增加折线条数,相应角的个数也会增多,∠B,∠E,∠F,∠G,∠D之间又会有何关系?
如图,AB∥DC,增加折线条数,相应角的个数也会增多,∠B,∠E,∠F,∠G,∠D之间又会有何关系?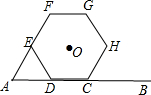 如图,已知线段AB=10,点D从A点开始沿AB边向右运动,以AD为边向上作正△ADE,再以DE为边向右作正六边形DEFGHC,点C恰好落在线段AB上,当C与B重合时运动结束,则正六边形的中心O的运动路径长为5$\sqrt{3}$,点B与点O的最短距离为5.
如图,已知线段AB=10,点D从A点开始沿AB边向右运动,以AD为边向上作正△ADE,再以DE为边向右作正六边形DEFGHC,点C恰好落在线段AB上,当C与B重合时运动结束,则正六边形的中心O的运动路径长为5$\sqrt{3}$,点B与点O的最短距离为5.