题目内容
2.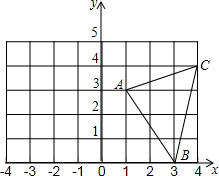 如图,在平面直角坐标系xOy中,
如图,在平面直角坐标系xOy中,(1)求出△ABC的面积和BC边上的高;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
分析 (1)利用“补全矩形法”求出△ABC的面积,求出BC的长,即可得出BC边上的高;
(2)分别找到A、B、C三点关于y轴的对称点,顺次连接可得△A1B1C1;
(3)结合直角坐标系可得点A1,B1,C1的坐标.
解答 解:(1)S△ABC=3×4-$\frac{1}{2}$×1×3-$\frac{1}{2}$×4×1-$\frac{1}{2}$×2×3=$\frac{11}{2}$,
∵BC=$\sqrt{17}$,
∴BC边上的高=$\frac{11}{\sqrt{17}}$=$\frac{11\sqrt{17}}{17}$.
(2)如图所示: .
.
(3)结合直角坐标系可得:A1(-1,3),B1(-3,0),C1(-4,4).
点评 本题考查了轴对称作图及三角形的面积,解答本题的关键是“补全矩形法”求三角形面积的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.小张上星期日买进某公司股票1000股,每股16元,下表为本周内每日该股票的涨跌情况(单位:元).
根据你所学的数学知识,解答下列各题:
(1)星期四收盘每股是多少元?
(2)本周内最高价每股多少元?最低是每股多少元?
(3)小张买进股票时付1.5‰的手续费,卖出时需付成交额1.5‰的手续费和1‰的交易税,如果小张在星期三收盘前将股票全部卖出,他的收益如何?
| 星 期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +3 | -2.5 | +3.5 | -1.5 | -4 |
(1)星期四收盘每股是多少元?
(2)本周内最高价每股多少元?最低是每股多少元?
(3)小张买进股票时付1.5‰的手续费,卖出时需付成交额1.5‰的手续费和1‰的交易税,如果小张在星期三收盘前将股票全部卖出,他的收益如何?
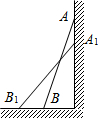 如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米.
如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米. 将连续的偶数2,4,6,8,…,排成如表:
将连续的偶数2,4,6,8,…,排成如表: 如图,△ABC绕点A逆时针旋转60°到△ADE的位置,点B的对应点是点D,点C的对应点是点E,已知∠BAC=125°,则∠DAC等于65°.
如图,△ABC绕点A逆时针旋转60°到△ADE的位置,点B的对应点是点D,点C的对应点是点E,已知∠BAC=125°,则∠DAC等于65°.