题目内容
13.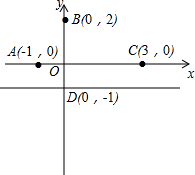 如图,在平面直角坐标系xOy中,已知点A(-1,0),点B(0,2),点C(3,0),直线a为过点D(0,-1)且平行于x轴的直线.
如图,在平面直角坐标系xOy中,已知点A(-1,0),点B(0,2),点C(3,0),直线a为过点D(0,-1)且平行于x轴的直线.(1)直接写出点B关于直线a对称的点E的坐标(0,-4);
(2)若P为直线a上一动点,请求出△PBA周长的最小值和此时P点坐标;
(3)若M为直线a上一动点,且S△ABC=S△MAB,请求出M点坐标.
分析 (1)根据点关于已知直线对称的点的特点即可得到结论;
(2)由B、E关于直线a对称,得到PB=PE,于是得到△PBA周长=AB+BP+PA=AB+PE+PA,根据两点之间线段最段,于是得到△PBA周长的最小值=AB+AE=$\sqrt{5}+\sqrt{17}$,求得直线AE的解析式:y=-4x-4,即可得到结论;
(3)设M(m,-1),由S△ABC=S△MAB,得到点M在过C且平行于AB的直线上,通过直线AB的解析式为:y=2x+2,设直线CM的解析式为:y=2x+n,即可得到结论.
解答 解:(1)∵B(0,2),D(0,-1),
∴BD=3,
∵直线a为过点D(0,-1)且平行于x轴的直线.
∴BD⊥直线a,
∴点B关于直线a对称的点E的坐标(0,-4);
故答案为:(0,-4);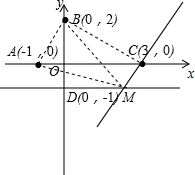
(2)∵B、E关于直线a对称,
∴PB=PE,
∴△PBA周长=AB+BP+PA
=AB+PE+PA
∵两点之间线段最段,
∴△PBA周长的最小值=AB+AE=$\sqrt{5}+\sqrt{17}$,
∴直线AE的解析式:y=-4x-4,
当y=-1时,x=$-\frac{3}{4}$,
∴P点坐标($-\frac{3}{4}$,-1);
(3)设M(m,-1),
当M在第四象限,
∵S△ABC=S△MAB,
∴点M在过C且平行于AB的直线上,
∵直线AB的解析式为:y=2x+2,
设直线CM的解析式为:y=2x+n,
∴0=2×3+n,
∴n=-6,
∴直线CM的解析式为:y=2x-6,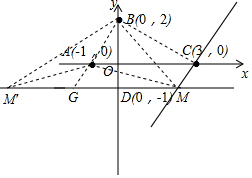
∴m=$\frac{5}{2}$,
∴M($\frac{5}{2}$,-1),
当M在第三象限,
直线AB与直线a交于G(-$\frac{3}{2}$,-1),
∴$\frac{1}{2}$×(-$\frac{3}{2}$-m)×(2+1)-$\frac{1}{2}$×(-$\frac{3}{2}$-m)×1=$\frac{1}{2}$×4×2,
∴m=-5.5,
∴M(-5.5,-1).
点评 此题主要考查了轴对称--最短路线问题,坐标与图形的性质,待定系数法求函数的解析式,正确的理解题意是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案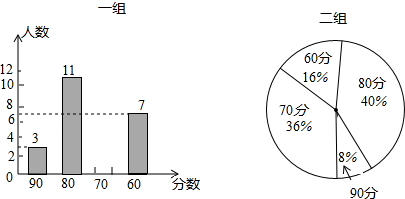
请你根据以上提供的信息解答下列问题:
(1)请你将表格补充完整:
| 平均数 | 中位数 | 众数 | 方差 | |
| 一组 | 74 | 80 | 80 | 104 |
| 二组 | 74 | 70 | 80 | 72 |
①两条不相交的直线叫做平行线;
②过直线外一点有且只有一条直线与已知直线垂直;
③若AB=BC,则点B是AC的中点;
④若两角的两边互相平行,则这两个角一定相等;
其中说法正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 如果x+7=26,那么x+5=24 | B. | 如果3x+2y=2x-y,那么3x+3y=2x | ||
| C. | 如果2a=5b,那么2ac=5bc | D. | 如果3x=4y,那么$\frac{3x}{{a}^{2}}$=$\frac{4y}{{a}^{2}}$ |
 如图,比较AB+BC与AC的大小关系是AB+BC>AC,它的根据是两点之间线段最短.
如图,比较AB+BC与AC的大小关系是AB+BC>AC,它的根据是两点之间线段最短.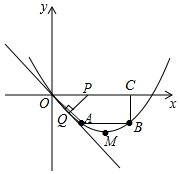 已知,如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.
已知,如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.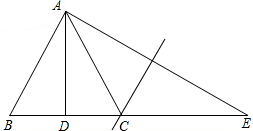 如图,△ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=12cm,则△ABC的周长是24cm.
如图,△ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=12cm,则△ABC的周长是24cm.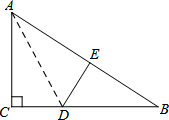 如图,折叠Rt△ABC,使直角边AC落在斜边AB上,点C落到点E处,已知AC=6cm,BC=8cm,则CD的长为( )
如图,折叠Rt△ABC,使直角边AC落在斜边AB上,点C落到点E处,已知AC=6cm,BC=8cm,则CD的长为( )