题目内容
8.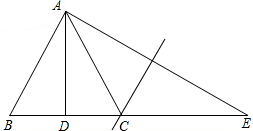 如图,△ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=12cm,则△ABC的周长是24cm.
如图,△ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=12cm,则△ABC的周长是24cm.
分析 根据线段垂直平分线上的点到线段两端点的距离相等可得AC=CE,根据等腰三角形三线合一的性质可得BD=CD,然后求出AD+BD=DE.
解答 解:∵点C在AE的垂直平分线上,
∴AC=CE,
∵AB=AC,AD平分∠BAC,
∴BD=CD,
∴AB+BD=AC+CD=CE+CD=DE,
∵DE=12cm,
∴AB+BC+AC=AB+BD+AC+CD=2×12=24cm.
故答案为:24cm.
点评 本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等腰三角形三线合一的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
2.方程-2x=$\frac{1}{2}$的解是( )
| A. | x=-$\frac{1}{4}$ | B. | x=$\frac{1}{4}$ | C. | x=-4 | D. | x=4 |
3.当温度恒定时,一定质量的气体压强P与体积V成反比,并且当体积为10升时,压强为2个大气压,则P(大气压)与V(升)的关系式为( )
| A. | P=20V | B. | P=5V | C. | PV=20 | D. | PV=5 |
16.如图1,在△ABC中,AB=AC,∠BAC=120°,点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
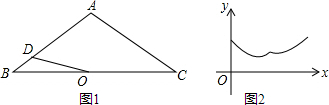

| A. | BD | B. | OD | C. | AD | D. | CD |
3.下列命题是真命题的是( )
| A. | 如果a2=b2,则a=b | |
| B. | 两边一角对应相等的两个三角形全等 | |
| C. | $\sqrt{81}$的算术平方根是9 | |
| D. | x=2,y=1是方程2x-y=3的解 |
20.下列各式中属于最简二次根式的是( )
| A. | $\sqrt{{x}^{2}y}$ | B. | $\sqrt{24}$ | C. | $\sqrt{{x}^{2}+1}$ | D. | $\sqrt{0.5}$ |
17.点(-3,2)向下平移3个单位长度,再向右平移4个单位长度后位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
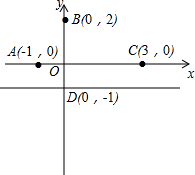 如图,在平面直角坐标系xOy中,已知点A(-1,0),点B(0,2),点C(3,0),直线a为过点D(0,-1)且平行于x轴的直线.
如图,在平面直角坐标系xOy中,已知点A(-1,0),点B(0,2),点C(3,0),直线a为过点D(0,-1)且平行于x轴的直线.