��Ŀ����
1�� ��ͼ����OBC��ֱ�������Σ�OB��x���������غϣ���OBC=90�㣬��OB=1��BC=$\sqrt{3}$������OBC��ԭ��O��ʱ����ת60���ٽ����������Ϊԭ����m����ʹOB1=OC���õ���OB1C1������OB1C1��ԭ��O��ʱ����ת60���ٽ����������Ϊԭ����m����ʹOB2=OC1���õ���OB2C2��������˼�����ȥ���õ���OB2017C2017����m��ֵ�͵�C2017�������ǣ�������
��ͼ����OBC��ֱ�������Σ�OB��x���������غϣ���OBC=90�㣬��OB=1��BC=$\sqrt{3}$������OBC��ԭ��O��ʱ����ת60���ٽ����������Ϊԭ����m����ʹOB1=OC���õ���OB1C1������OB1C1��ԭ��O��ʱ����ת60���ٽ����������Ϊԭ����m����ʹOB2=OC1���õ���OB2C2��������˼�����ȥ���õ���OB2017C2017����m��ֵ�͵�C2017�������ǣ�������| A�� | 2����-22017��22017��$\sqrt{3}$�� | B�� | 2����-22018��0�� | ||
| C�� | $\sqrt{3}$����-22017��22017��$\sqrt{3}$�� | D�� | $\sqrt{3}$����-22018��0�� |
���� �Ƚ�ֱ�������������BOC=60�㣬�ٸ���30������Ե�ֱ�DZߵ���б�ߵ�һ�뼴�����m��ֵ������ֱ�������εó���BOC=60�㣬Ȼ�����OC1��OC2��OC3������OCn�ij��ȣ��ٸ����ܽǵ���360�㣬ÿ6��Ϊһ��ѭ���飬�����C2017�ǵڼ���ѭ����ĵڼ����㣬�ٸ��ݱ仯����д��������꼴�ɣ�
��� 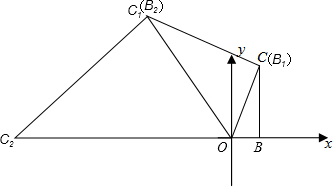 ��⣺�ߡ�OBC=90�㣬OB=1��BC=$\sqrt{3}$��
��⣺�ߡ�OBC=90�㣬OB=1��BC=$\sqrt{3}$��
��tan��BOC=$\frac{BC}{OB}$=$\sqrt{3}$��
���BOC=60�㣬
��OC=2OB=2��1=2��
�߽���OBC��ԭ��O��ʱ����ת60���ٽ����������Ϊԭ����m����ʹOB1=OC��
��m=2��
�ߡ�OBC=90�㣬OB=1��BC=$\sqrt{3}$��
�߽���OBC��ԭ��O��ʱ����ת60���ٽ����������Ϊԭ����2����ʹOB1=OC��
��OC1=2OC=2��2=4=22��
OC2=2OC1=2��4=8=23��
OC3=2OC2=2��8=16=24��
����
OCn=2n+1��
��OC2015=22016��
��2017��6=336��1��
���C2017���C1��ͬһ�����ϣ��ڵڶ����ޣ�����Ϊ��-22017��22017��$\sqrt{3}$����
��ѡA��
���� ���⿼����������ͼ�εı仯-��ת����ֱ�������Σ����ݽ�ֱ�������Σ��Լ�30������Ե�ֱ�DZߵ���б�ߵ�һ�룬���m��ֵ�ǽ���Ĺؼ���

 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�| A�� | -2 | B�� | 2 | C�� | -10 | D�� | 2 |
| A�� | sinA=$\frac{c}{a}$ | B�� | cosB=$\frac{b}{c}$ | C�� | sinB=$\frac{b}{a}$ | D�� | tanA=$\frac{a}{b}$ |