题目内容
7.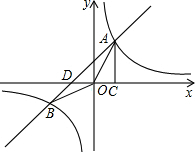 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+1的图象相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+1的图象相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,(1)反比例函数的解析式为y=$\frac{2}{x}$.(直接写出结果)
(2)求它们的两个交点A,B的坐标.
(3)观察图象写出使反比例函数的值大于一次函数的值的x的取值范围.
(4)求△AOB的面积.
分析 (1)由△OAC的面积为1,直接得出k的数值为2,写出函数解析式即可;
(2)两个函数联立方程求得方程的根即可;
(3)根据图象的两个交点坐标直接得出答案即可;
(4)求得一次函数与x轴的交点D坐标,利用三角形的面积计算公式求得答案即可.
解答 解:(1)反比例函数的解析式为y=$\frac{2}{x}$;
(2)由题意得x+1=$\frac{2}{x}$
解得:x=1或x=-2,
则对应y=2或y=-1,
∴两个交点A为(1,2),B为(-2,-1);
(3)由图象可知反比例函数的值大于一次函数的值的x的取值范围为:x<-2或0<x1.
(4)由y=x+1得与x轴的交点D(-1,0),
S△AOB=S△BOD+S△AOD
=$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×2
=1.5.
点评 此题考查反比例函数与一次函数的交点问题,求出反比例函数的解析式是解答本题的关键.

练习册系列答案
相关题目
2. 如图,AB∥CD,点E在BC上,CD=CE,若∠ABC=34°,则∠BED的度数是( )
如图,AB∥CD,点E在BC上,CD=CE,若∠ABC=34°,则∠BED的度数是( )
 如图,AB∥CD,点E在BC上,CD=CE,若∠ABC=34°,则∠BED的度数是( )
如图,AB∥CD,点E在BC上,CD=CE,若∠ABC=34°,则∠BED的度数是( )| A. | 104° | B. | 107° | C. | 116° | D. | 124° |
 如图,扇形OAB是圆锥的侧面展开图,若OA=4$\sqrt{2}$cm,OA⊥OB,则这个圆锥的底面半径为$\sqrt{2}$cm.
如图,扇形OAB是圆锥的侧面展开图,若OA=4$\sqrt{2}$cm,OA⊥OB,则这个圆锥的底面半径为$\sqrt{2}$cm.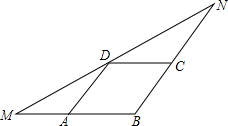 如图,在△MBN中,BM=6,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则?ABCD的周长是( )
如图,在△MBN中,BM=6,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则?ABCD的周长是( ) 如图,将三角形ABC沿BC方向平移acm得到三角形DEF,若△ABC的周长为bcm,则四边形ABFD的周长为(b+2a)cm(用含a,b的式子表示)
如图,将三角形ABC沿BC方向平移acm得到三角形DEF,若△ABC的周长为bcm,则四边形ABFD的周长为(b+2a)cm(用含a,b的式子表示)