题目内容
3.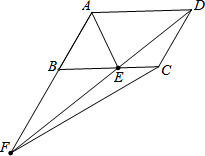 如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=2cm,则△CEF面积是$\sqrt{3}$cm2.
如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=2cm,则△CEF面积是$\sqrt{3}$cm2.
分析 由平行四边形的性质和角平分线的定义得出∠BAE=∠BEA,得出AB=BE=AE,所以△ABE是等边三角形,由AB的长,可求出△ABE的面积,再根据△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),可得S△FCD=S△ABC,又因为△AEC与△DEC同底等高,所以S△AEC=S△DEC,即S△ABE=S△CEF问题得解.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EAD=∠AEB,
又∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形,
∵AB=2cm,
∴△ABE的面积=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$cm2,
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),
∴S△FCD=S△ABC,
又∵△AEC与△DEC同底等高,
∴S△AEC=S△DEC,
∴S△ABE=S△CEF=$\sqrt{3}$cm2,
故答案为:$\sqrt{3}$
点评 此题考查了平行四边形的性质、等边三角形的判定与性质、三角形的面积关系,解题的关键是首先证明△ABE是等边三角形,求△CEF的面积转化为求△ABE的面积.

练习册系列答案
相关题目
13.已知一个多边形的内角和等于它的外角和的3倍,那么它的边数是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
14.若2x=3,2y=5,则2x-y的值为( )
| A. | $\frac{6}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{10}$ | D. | -2 |
 如图,在已知平行四边形ABCD中,AE平分∠BAD,与BC相交于点E,EF∥AB,与AD相交于点F.求证:四边形ABEF是菱形.
如图,在已知平行四边形ABCD中,AE平分∠BAD,与BC相交于点E,EF∥AB,与AD相交于点F.求证:四边形ABEF是菱形. 如图,扇形OAB是圆锥的侧面展开图,若OA=4$\sqrt{2}$cm,OA⊥OB,则这个圆锥的底面半径为$\sqrt{2}$cm.
如图,扇形OAB是圆锥的侧面展开图,若OA=4$\sqrt{2}$cm,OA⊥OB,则这个圆锥的底面半径为$\sqrt{2}$cm.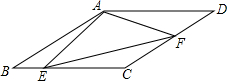 如图,AB∥CD,AD∥BC,点E、F分别是线段BC和CD上的动点,在两点运动到某一位置时,恰好使得∠AEF=∠AFE,此时量得∠BAE=15°,∠FEC=12°,∠DAF=25°,则∠EFC=22°.
如图,AB∥CD,AD∥BC,点E、F分别是线段BC和CD上的动点,在两点运动到某一位置时,恰好使得∠AEF=∠AFE,此时量得∠BAE=15°,∠FEC=12°,∠DAF=25°,则∠EFC=22°.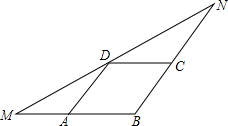 如图,在△MBN中,BM=6,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则?ABCD的周长是( )
如图,在△MBN中,BM=6,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则?ABCD的周长是( )