题目内容
5.关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;②(m-1)2+(n-1)2≥2;③-1≤2m-2n≤1,其中正确结论的个数是( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①根据题意,以及根与系数的关系,可知两个整数根都是负数;②根据根的判别式,以及题意可以得出m2-2n≥0以及n2-2m≥0,进而得解;③可以采用根与系数关系进行解答,据此即可得解.
解答 解:①两个整数根且乘积为正,两个根同号,由韦达定理有,x1•x2=2n>0,y1•y2=2m>0,
y1+y2=-2n<0,
x1+x2=-2m<0,
这两个方程的根都为负根,①正确;
②由根判别式有:
△=b2-4ac=4m2-8n≥0,△=b2-4ac=4n2-8m≥0,
∵4m2-8n≥0,4n2-8m≥0,
∴m2-2n≥0,n2-2m≥0,
m2-2m+1+n2-2n+1=m2-2n+n2-2m+2≥2,
(m-1)2+(n-1)2≥2,②正确;
③由根与系数关系可得2m-2n=y1y2+y1+y2=(y1+1)(y2+1)-1,
由y1、y2均为负整数,故(y1+1)•(y2+1)≥0,故2m-2n≥-1,
同理可得:2n-2m=x1x2+x1+x2=(x1+1)(x2+1)-1,得2n-2m≥-1,即2m-2n≤1,故③正确.
故选:D.
点评 本题主要考查了根与系数的关系,以及一元二次方程的根的判别式,有一定的难度,注意总结.

练习册系列答案
相关题目
16.计算a3•($\frac{1}{a}$)2的结果是( )
| A. | a | B. | a5 | C. | a6 | D. | a8 |
13. 如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
 如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )| A. | x>-2 | B. | x<-2 | C. | -3<x<-2 | D. | -3<x<-1 |
20.两个相似多边形的面积之比为1:9,则它们的周长之比为( )
| A. | 1:3 | B. | 1:9 | C. | 1:$\sqrt{3}$ | D. | 2:3 |
10. 如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )
如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )
 如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )
如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )| A. |  | B. | 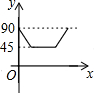 | C. |  | D. |  |
14.甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别中A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200);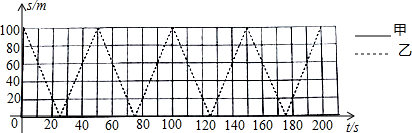
(2)根据(1)中所画图象,完成下列表格:
(3)①直接写出甲、乙两人分别在第一个100m内,s与t的函数解析式,并指出自变量t的取值范围;
②当t=390s时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A端的距离.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200);

(2)根据(1)中所画图象,完成下列表格:
| 两人相遇次数 (单位:次) | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和 (单位:m) | 100 | 300 | 500 | 700 | … | 200n-100 |
②当t=390s时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A端的距离.
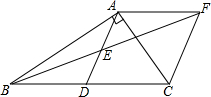 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.