题目内容
13.求关于x,y的方程组$\left\{\begin{array}{l}{3y+2x=100-2a}\\{3y-2x=20}\end{array}\right.$的正整数解,其中a为不小于24的正整数.分析 先把a当作已知条件表示出x,y的值,再根据x,y是正整数及a为不小于24的正整数求出a的值,再代入x、y的表达式即可得出结论.
解答 解:$\left\{\begin{array}{l}{3y+2x=100-2a①}\\{3y-2x=20②}\end{array}\right.$,
①+②得:6y=120-2a,即y=20-$\frac{1}{3}$a,
①-②得:4x=80-2a,即x=20-$\frac{1}{2}$a,
∵x,y是正整数,
∴y>0,x>0,即$\left\{\begin{array}{l}20-\frac{1}{3}a>0\\ 20-\frac{1}{2}a>0\end{array}\right.$,解得a<40.
∵a为不小于24的正整数,
∴24≤a<40,且a是6的倍数,
∴a=24,30,36.
当a=24时,$\left\{\begin{array}{l}x=8\\ y=12\end{array}\right.$;当a=30时,$\left\{\begin{array}{l}x=5\\ y=10\end{array}\right.$;当a=36时,$\left\{\begin{array}{l}x=2\\ y=8\end{array}\right.$.
点评 本题考查的是二元一次方程组得解,先根据题意得出a的值是解答此题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
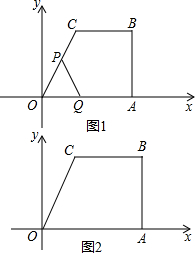 如图,在梯形OABC中,OA∥BC,∠B=90°,OC=10,BC=8,AB=8.以O为原点,OA为x轴建立平面直角坐标系.P、Q同时从点O出发,点P以1单位/s的速度沿折线OC→CB→BA向A点匀速运动,点Q以1单位/s的速度沿x轴的正半轴方向匀速运动.当点P到达点A时,点Q也随之停止运动.设运动时间为t秒.
如图,在梯形OABC中,OA∥BC,∠B=90°,OC=10,BC=8,AB=8.以O为原点,OA为x轴建立平面直角坐标系.P、Q同时从点O出发,点P以1单位/s的速度沿折线OC→CB→BA向A点匀速运动,点Q以1单位/s的速度沿x轴的正半轴方向匀速运动.当点P到达点A时,点Q也随之停止运动.设运动时间为t秒.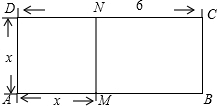 我们知道:x2-6x=(x2-6x+9)-9=(x-3)2-9;-x2+10=-(x2-10x+25)+25=-(x-5)2+25,这一种方法称为配方法,利用配方法请解以下各题:
我们知道:x2-6x=(x2-6x+9)-9=(x-3)2-9;-x2+10=-(x2-10x+25)+25=-(x-5)2+25,这一种方法称为配方法,利用配方法请解以下各题: 如图,△ABC≌△ADE,BC=DE,∠B=100°,∠BAC=40°那么∠AED=40°.
如图,△ABC≌△ADE,BC=DE,∠B=100°,∠BAC=40°那么∠AED=40°.