题目内容
4. 某服装厂批发应夏季T恤衫,其单价y(元)与批发数量x(件)(x为正整数)之间的函数关系如图所示,
某服装厂批发应夏季T恤衫,其单价y(元)与批发数量x(件)(x为正整数)之间的函数关系如图所示,(1)直接写出y与x的函数关系式;
(2)一个批发商一次购进250件T恤衫,所花的钱数是多少元?(其他费用不计);
(3)若每件T恤衫的成本价是20元,当100<x≤400件,(x为正整数)时,求服装厂所获利润w (元)与x(件)之间的函数关系式,并求一次批发多少件时所获利润最大,最大利润是多少?
分析 (1)由题意设出一次函数的解析式,再根据点在直线上待定系数法求出函数解析式;
(2)列出总利润的函数表达式,转化为求函数最值问题,最后求出最大利润;
(3)根据利润=单件利润×批发数量,列出二次函数表达式,再运用二次函数性质解决最值问题.
解答 解:(1)当0≤x<100时,y=60;
当x≥100时,设y=kx+b,由图象可以看出过(100,60),(400,40),则
$\left\{\begin{array}{l}{100k+b=60}\\{400k+b=40}\end{array}\right.$,
$\left\{\begin{array}{l}{k=-\frac{1}{15}}\\{b=\frac{200}{3}}\end{array}\right.$,
∴y=$\left\{\begin{array}{l}{60(0≤x<100)}\\{-\frac{1}{15}x+\frac{200}{3}(x≥100)}\end{array}\right.$;
(2)∵250>100,
∴当x=250件时,y=-$\frac{1}{15}$×250+$\frac{200}{3}$=50元,
∴批发商一次购进250件T恤衫,所花的钱数是:50×250=12500元;
(3)W=(-$\frac{1}{15}$x+$\frac{200}{3}$-20)×x=-$\frac{1}{15}$x2+$\frac{140}{3}$x=-$\frac{1}{15}$(x-350)2+$\frac{24500}{3}$,
∴当一次性批发350件时,所获利润最大,最大利润是$\frac{24500}{3}$元.
点评 本题考查了待定系数法求函数关系式以及运用函数的性质解决问题,根据题意列出函数表达式是解决问题的关键.

| A. | 33.5×109 | B. | 33.5×1012 | C. | 33.5×1012 | D. | 3.35×1013 |
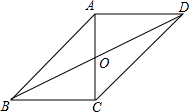 如图,在△ABC中,∠ACB=90°,AC=BC=1cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在点D处,连接BD,那么线段BD的长为$\sqrt{5}$cm.
如图,在△ABC中,∠ACB=90°,AC=BC=1cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在点D处,连接BD,那么线段BD的长为$\sqrt{5}$cm.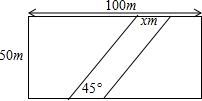 如图,在草坪中间修一条小路,小路的横向宽为x m,设开辟道路后草地的实际面积为y m2.
如图,在草坪中间修一条小路,小路的横向宽为x m,设开辟道路后草地的实际面积为y m2.