题目内容
6．
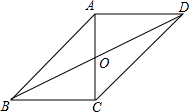如图，在△ABC中，∠ACB=90°，AC=BC=1cm，如果以AC的中点O为旋转中心，将△ABC旋转180°，点B落在点D处，连接BD，那么线段BD的长为$\sqrt{5}$cm．
分析 根据旋转的性质可知，点B与D重合，那么点D与点B的距离是2OB，由勾股定理可得OB的大小．
解答 解：如图，∵∠C=90°，AC=BC=1cm，O为AC的中点，
∴OB=$\frac{\sqrt{5}}{2}$，
∵根据旋转的性质可知，点B与D重合，
∴BD=2OB=$\sqrt{5}$cm．
故答案为$\sqrt{5}$．
点评 此题主要考查等腰直角三角形的性质和旋转的性质，得出BD=2OB是关键．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
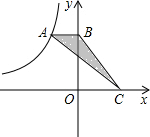如图，A为反比例图象上一点，AB⊥y轴于点B，C点是x轴上一点，S△ABC=1，则这个反比例函数为y=-$\frac{2}{x}$．
如图，三角形ABC中，线段AF与射线DE交于点P，其中点D、F在BC上，点E在射线AC上，点P′在射线DE上，平移三角形ABC，使点P移动到点P′．
某服装厂批发应夏季T恤衫，其单价y（元）与批发数量x（件）（x为正整数）之间的函数关系如图所示，