题目内容
9.先化简再求值:(x+2)(x-2)-(x+2)2,其中x=$\frac{1}{2}$.分析 先根据完全平方公式和平方差公式算乘法,再合并同类项,最后代入求出即可.
解答 解:原式=x2-4-(x2+4x+4)
=x2-4-x2-4x-4
=-4x-8,
当x=$\frac{1}{2}$时,原式=-4×$\frac{1}{2}$-8=-10.
点评 本题考查了整式的混合运算和求值的应用,能根据整式的运算法则进行化简是解此题的关键,难度适中.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
20.-6是( )
| A. | 负有理数 | B. | 正有理数 | C. | 自然数 | D. | 无理数 |
4.下列式子$\frac{1}{x}$、$\frac{1}{2}$、$\frac{x+1}{3}$、$\frac{5}{m}$、$\frac{3}{x+y}$中,属于分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.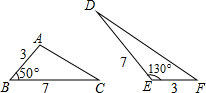 如图,若△ABC和△DEF的面积分别为S1,S2,则( )
如图,若△ABC和△DEF的面积分别为S1,S2,则( )
 如图,若△ABC和△DEF的面积分别为S1,S2,则( )
如图,若△ABC和△DEF的面积分别为S1,S2,则( )| A. | S1=$\frac{1}{2}$S2 | B. | S1=$\frac{7}{2}$S2 | C. | S1=$\frac{8}{5}$S2 | D. | S1=S2 |

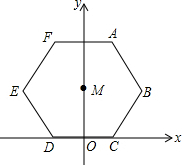 如图,一个边长为2的正六边形ABCDEF的边CD在x轴上,正六边形的中心M在y轴上,现在把这个正六边形沿x轴无滑动的滚动一周,则顶点A的坐标为(13,2$\sqrt{3}$),若滚动100周,中心M经过的路径长400π.
如图,一个边长为2的正六边形ABCDEF的边CD在x轴上,正六边形的中心M在y轴上,现在把这个正六边形沿x轴无滑动的滚动一周,则顶点A的坐标为(13,2$\sqrt{3}$),若滚动100周,中心M经过的路径长400π.