题目内容

16．已知菱形周长为20，两对角线之比为4：3，则菱形面积为24．

分析 根据已知可分别求得两条对角线的长，再根据菱形的面积等于两对角线乘积的一半即可得到其面积．

解答 解：设两条对角线长分别为4x，3x，
根据勾股定理可得（2x）2+（$\frac{3}{2}$x）2=52，
解之得，x=2，
则两条对角线长分别为8、6，
∴菱形的面积=8×6÷2=24．
故答案为24．

点评 本题考查了菱形的性质，主要要掌握菱形的面积公式：两条对角线的积的一半，综合利用了菱形的性质和勾股定理．

练习册系列答案
相关题目
6．下列图形一定是相似图形的是（　　）
A．任意两个菱形B．任意两个正三角形
C．两个等腰三角形D．两个矩形
7．写出同时具备下列两个条件的一次函数表达式（写出一个即可）y=-x+2
（1）y随x的增大而减小；
（2）图象经过点（0，2）
4．已知点P的坐标（2a，6-a），且点P到两坐标轴的距离相等，则点P的坐标是（　　）
A．（12，-12）或（4，-4）B．（-12，12）或（4，4）C．（-12，12）D．（4，4）
11．计算：22015×（-0.5）2016=0.5．
1．如图，在△ABD中，C是BD上一点，若E、F分别是AC、AB的中点，△DEF的面积为4.5，则△ABC的面积为18．
8．定义{a，b，c}为函数y=ax2+bx+c的“特征数”．
（1）“特征数”为{-1，2，3}的函数解析式为y=-x2+2x+3，将“特征数”为{0，1，1}的函数向下平移两个单位以后得到的函数解析式为y=x-1；
（2）我们把横、纵坐标均为整数的点称为“整点”，试问：在上述两空填写的函数图象围成的封闭图形（包含边界）内共有多少个整点？请给出详细的运算过程；
（3）定义“特征数”的运算：①{a1，b1，c1}+{a2，b2，c2}={a1+a2，b1+b2，c1+c2}；②λ•{a1，b1，c1}={λa1，λb1，λc1}（其中λ为任意常数）．试问：“特征数”为{-1，2，3}+λ•{0，1，-1}的函数是否过定点？如果过定点，请计算出该定点坐标；如果不存在，请说明你的理由．
5．如果一个空间几何体的主视图和左视图都是边长为4的正三角形，俯视图是圆且中间有一点，那么这个几何体的表面积是（　　）
A．8πB．12πC．4$\sqrt{3}$πD．8
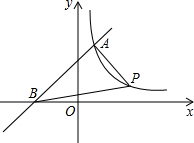6．如图，一次函数y=x+3与反比例函数y=$\frac{k}{x}$（x＞0）的图象相交于点A（m，4），与x轴相交于点B．
（1）求反比例函数的解析式；
（2）若点p在双曲线上，且△PAB为直角三角形（∠BAP=90°），则点p的坐标是（4，1）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网