题目内容
4.已知点P的坐标(2a,6-a),且点P到两坐标轴的距离相等,则点P的坐标是( )| A. | (12,-12)或(4,-4) | B. | (-12,12)或(4,4) | C. | (-12,12) | D. | (4,4) |
分析 根据点到两坐标轴的距离相等列出绝对值方程求出a的值,然后求解即可.
解答 解:∵点P(2a,6-a)到两坐标轴的距离相等,
∴|2a|=|6-a|,
∴2a=6-a或2a=-(6-a),
解得a=2或a=-6,
当a=2时,2a=2×2=4,6-a=6-2=4,
此时,点P的坐标为(4,4),
当a=-6时,2a=2×(-6)=-12,6-(-6)=6+6=12,
此时,点P的坐标为(-12,12),
综上所述,点P的坐标为(-12,12)或(4,4).
故选B.
点评 本题考查了点的坐标,难点在于根据点到坐标轴的距离列出绝对值方程并求解.

练习册系列答案
相关题目
19.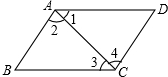 如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )
如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )
 如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )
如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )| A. | ∠1=∠3 | B. | ∠2=∠4 | C. | ∠B=∠D | D. | ∠1+∠2+∠B=180° |
13.若点P是线段MN的中点,则下列结论不正确的是( )
| A. | MP=NP | B. | MN=2NP | C. | MP=$\frac{1}{2}$MN | D. | MN=$\frac{1}{2}$NP |
 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°,BD=3,CE=2,则△ABC的边长为9.
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°,BD=3,CE=2,则△ABC的边长为9.