题目内容
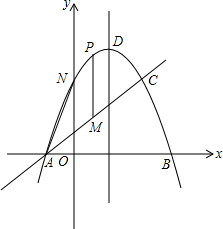 如图,已知抛物线y=-x2+2x+3与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N,抛物线的对称轴是直线x=1,其顶点为D(1,4)
如图,已知抛物线y=-x2+2x+3与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N,抛物线的对称轴是直线x=1,其顶点为D(1,4)(1)若点P是直线AC上方抛物线上的一个动点,过点P作PM∥y轴,交直线AC于点M,当线段PM的长度最大时,请求出最大值及点P的坐标
(2)连接AN,在抛物线的对称轴上是否存在点E,使∠EAC=∠ANO,若存在,请求出点E的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)代入A,C两点可求得直线AC解析式,根据PM=-x2+2x+3-(x+1)即可解题;
(2)存在2种情况:①∠EAC=∠ANO,②∠E'AC=∠ANO,即可求得tan∠EAB的值,即可求得直线AE斜率,根据直线经过A点即可求得直线AE解析式,即可求得直线和抛物线交点,即可解题.
(2)存在2种情况:①∠EAC=∠ANO,②∠E'AC=∠ANO,即可求得tan∠EAB的值,即可求得直线AE斜率,根据直线经过A点即可求得直线AE解析式,即可求得直线和抛物线交点,即可解题.
解答:解:(1)设点P坐标为(x,y),
∵直线AC经过A,C两点,设直线AC解析式为y=kx+b,
则有
,
解得:k=1,b=1,
∴直线AC解析式为y=x+1,
∴线段PM长度=-x2+2x+3-x-1=-x2+x+2,
∴当x=-
=
时,线段PM长度有最大值为
;
(2)存在2种情况:

①∠EAC=∠ANO,
∵∠CAB=45°,
∴tan∠CAB=1,
∵tan∠ANO=
,
∴tan∠EAC=
,
∴tan∠EAB=tan(∠CAB-∠EAC)=
=
,
∵直线AE经过点A,
∴直线AE解析式为:y=
x+
,
∴点E坐标为:(
,
);
②∠E′AC=∠ANO,
∵∠CAB=45°,
∴tan∠CAB=1,
∵tan∠ANO=
,
∴tan∠E'AC=
,
∴tan∠E'AB=tan(∠CAB+∠E'AC)=
=2,
∵直线AE经过点A,
∴直线AE解析式为:y=2x+2,
∴点E坐标为:(1,4);
∴存在点E,坐标为(1,4)或(
,
).
∵直线AC经过A,C两点,设直线AC解析式为y=kx+b,
则有
|
解得:k=1,b=1,
∴直线AC解析式为y=x+1,
∴线段PM长度=-x2+2x+3-x-1=-x2+x+2,
∴当x=-
| b |
| 2a |
| 1 |
| 2 |
| 5 |
| 2 |
(2)存在2种情况:

①∠EAC=∠ANO,
∵∠CAB=45°,
∴tan∠CAB=1,
∵tan∠ANO=
| 1 |
| 3 |
∴tan∠EAC=
| 1 |
| 3 |
∴tan∠EAB=tan(∠CAB-∠EAC)=
1-
| ||
1+
|
| 1 |
| 2 |
∵直线AE经过点A,
∴直线AE解析式为:y=
| 1 |
| 2 |
| 1 |
| 2 |
∴点E坐标为:(
| 5 |
| 2 |
| 7 |
| 4 |
②∠E′AC=∠ANO,
∵∠CAB=45°,
∴tan∠CAB=1,
∵tan∠ANO=
| 1 |
| 3 |
∴tan∠E'AC=
| 1 |
| 3 |
∴tan∠E'AB=tan(∠CAB+∠E'AC)=
1+
| ||
1-
|
∵直线AE经过点A,
∴直线AE解析式为:y=2x+2,
∴点E坐标为:(1,4);
∴存在点E,坐标为(1,4)或(
| 5 |
| 2 |
| 7 |
| 4 |
点评:本题考查了抛物线解析式的求解,考查了抛物线和直线交点的求解,考查了三角函数的运用,本题中求得直线AE的解析式是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
下列说法正确的是( )
| A、数据1,2,3,2,5的中位数是3 |
| B、数据5,5,7,5,7,6,11的众数是7 |
| C、若甲组数据方差S2甲=0.15,乙组数据方差S2乙=0.15,则乙组数据比甲组数据稳定 |
| D、数据1,2,2,3,7的平均数是3 |
 有理数a,b在数轴上的位置如图所示,化简3a-2b+3|a+b|的结果是( )
有理数a,b在数轴上的位置如图所示,化简3a-2b+3|a+b|的结果是( )| A、2a+2b | B、5b |
| C、-5b | D、0 |