题目内容
设m是不小于-1的实数,使得关于x的方程x2+2(m-2)x+m2-3m+3=0有两个不相等的实数根x1,x2
(1)若
+
=1,求
的值;
(2)当m为何值时,代数式
+
-m2的值为3.
(1)若
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| 3-2m |
(2)当m为何值时,代数式
| mx1 |
| 1-x1 |
| mx2 |
| 1-x2 |
考点:根与系数的关系,根的判别式
专题:
分析:(1)首先根据根的判别式求出m的取值范围,利用根与系数的关系,求出符合条件的m的值;
(2)把利用根与系数的关系得到的关系式代入代数式,建立方程求得数值.
(2)把利用根与系数的关系得到的关系式代入代数式,建立方程求得数值.
解答:解:∵方程有两个不相等的实数根,
∴△=b2-4ac=4(m-2)2-4(m2-3m+3)=-4m+4>0,
∴m<1,
结合题意知:-1≤m<1.
(1)∵x1+x2=-2(m-2),x1x2=m2-3m+3,
∴
+
=
=
=1
解得:m1=
,m2=
(不合题意,舍去)
∴
=
-2.
(2)
+
-m2=
-m2
=-2(m-1)-m2
=-(m+1)2+3=3
解得:m=-1.
即当m=-1,代数式
+
-m2的值为3.
∴△=b2-4ac=4(m-2)2-4(m2-3m+3)=-4m+4>0,
∴m<1,
结合题意知:-1≤m<1.
(1)∵x1+x2=-2(m-2),x1x2=m2-3m+3,
∴
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| -2(m-2) |
| m2-3m+3 |
解得:m1=
1-
| ||
| 2 |
1+
| ||
| 2 |
∴
| 1 |
| 3-2m |
| 5 |
(2)
| mx1 |
| 1-x1 |
| mx2 |
| 1-x2 |
| m(x1+x2)-2mx1x2 |
| 1-x1x2+x1+x2 |
=-2(m-1)-m2
=-(m+1)2+3=3
解得:m=-1.
即当m=-1,代数式
| mx1 |
| 1-x1 |
| mx2 |
| 1-x2 |
点评:此题考查根与系数的关系,一元二次方程的根的判别式△=b2-4ac来求出m的取值范围;解答此题的关键是熟知一元二次方程根与系数的关系:x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
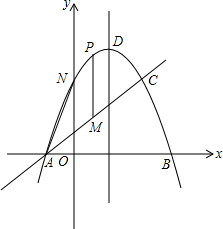 如图,已知抛物线y=-x2+2x+3与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N,抛物线的对称轴是直线x=1,其顶点为D(1,4)
如图,已知抛物线y=-x2+2x+3与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N,抛物线的对称轴是直线x=1,其顶点为D(1,4)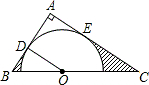 如图,在△ABC中,∠A=90°,O是BC边上的一点,以点O为圆心的分分别与边AB,AC相切于点D,E连接OD,已知BD=2,AD=3.求阴影部分的面积.
如图,在△ABC中,∠A=90°,O是BC边上的一点,以点O为圆心的分分别与边AB,AC相切于点D,E连接OD,已知BD=2,AD=3.求阴影部分的面积.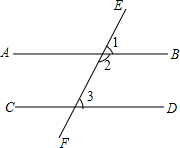 已知∠2=3∠1且∠1+∠3=90°,试说明AB∥CD.
已知∠2=3∠1且∠1+∠3=90°,试说明AB∥CD.