题目内容
16.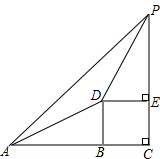 山顶上有一个电视铁塔,从地面A点看铁塔顶P的仰角是45°,沿坡度i=1:$\sqrt{3}$的山坡向 上走了100米,到达D点,再看铁塔顶P的仰角是60°,求铁塔顶P到地面的距离PC(结果保留根号).
山顶上有一个电视铁塔,从地面A点看铁塔顶P的仰角是45°,沿坡度i=1:$\sqrt{3}$的山坡向 上走了100米,到达D点,再看铁塔顶P的仰角是60°,求铁塔顶P到地面的距离PC(结果保留根号).
分析 根据坡度i=1:$\sqrt{3}$,求出∠DAB的度数,根据题意求出AB和BD的长度,设DE=x,根据三角函数的定义表示出AC和PC,列出方程,解方程得到答案.
解答 解:∵AD的坡度i=1:$\sqrt{3}$,
∴∠DAB=30°,又AD=100,
∴AB=50$\sqrt{3}$,BD=50,则CE=BD=50,
设DE=x,则BC=x,
∵∠PDE=60°,∴PE=$\sqrt{3}$x,
∵∠PAC=45°,
∴AC=PC,即50$\sqrt{3}$+x=50+$\sqrt{3}$x,
解得,x=50,则PE=$\sqrt{3}$x=50$\sqrt{3}$,
PC=PE+EC=50$\sqrt{3}$+50米.
答:铁塔顶P到地面的距离PC为50$\sqrt{3}$+50米.
点评 本题考查的是解直角思想的应用,掌握仰角和坡度的概念、正确运用锐角三角函数的概念是解题的关键.

练习册系列答案
相关题目
7.已知点(-2,5),(4,5)是抛物线上的两点,则此抛物线的对称轴为( )
| A. | x=-2 | B. | x=2 | C. | x=1 | D. | 无法确定 |
4.n边形的边数每增加一条,其对角线增加( )
| A. | n条 | B. | (n-1)条 | C. | (n-2)条 | D. | (n-3)条 |
6.将二次函数y=x2-2x+3化为y=a(x+h)2+k的形式,结果为( )
| A. | y=(x+1)2+2 | B. | y=(x-1)2+4 | C. | y=(x+1)2+4 | D. | y=(x-1)2+2 |
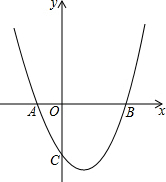 如图所示,二次函数y=x2+bx+c的图象经过点A(-1,0)和B(3,0),且与y轴交于点C.
如图所示,二次函数y=x2+bx+c的图象经过点A(-1,0)和B(3,0),且与y轴交于点C.