题目内容
在平面直角坐标系xOy中,以原点O为圆心半径为10的圆,直线y=mx-4m+3与⊙O交于A、B两点,则弦AB的长的最小值为

【解析】
试题分析:根据题意画出图形,因为直线y=mx-4m+3必过点D(4,3),求出最短的弦CB是过点D且与该圆直径垂直的弦,再求出OD的长,再根据以原点O为圆心的圆过点A(10,0),求出OB的长,再利用勾股定理求出BD,即可得出答案.
试题解析:∵直线y=mx-4m+3必过点D(4,3),
∴最短的弦CB是过点D且与该圆直径垂直的弦,

∵点D的坐标是(4,3),
∴OD=5,
∵⊙O的半径为10,
∴A(10,0),
∴OB=10,
∴BD= ,
,
∴BC的长的最小值为
考点:1.垂径定理;2.一次函数图象上点的坐标特征;3.勾股定理.

练习册系列答案
相关题目
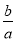 ,x1•x2=
,x1•x2=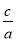 .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=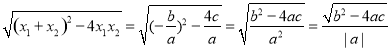 ;
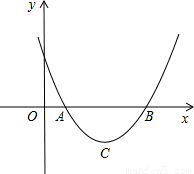
;

 ,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
 B.k≥
B.k≥ (x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,
(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,